By the bar, you find a relaxing-looking card game, Uno Royale. It's just like regular Uno, but with a competitive edge and simplified rules:

1. You and the dealer each start with ~m~ cards. Each card has a color and a number.
2. The dealer goes first, playing any one of their cards to start the pile.
3. Then, you and the dealer take turns, one after the other, playing cards onto the pile. You may only play a card if it satisfies either of the following conditions:
   • It has the same color as the current top card and a greater number.
   • It has the same number as the current top card (regardless of color).
4. The game ends when a player cannot legally play a card on their turn. This includes running out of cards.

After a few thrilling rounds of Uno Royale, you're hooked. Now, you want each game to last as long as possible.

Given the starting hands of both you and the dealer, determine the maximum number of cards that can be played in a single game, assuming both players make optimal moves to prolong the game.

Input

The first line consists of an integer ~m~ ~(1 \leq m \leq 10^5)~, the number of cards you and the dealer start with.

The next ~m~ lines contain ~C_{d,i}~ and ~n_{d,i}~, indicating that the dealer has a card with color ~C_{d,i}~ and number ~n_{d,i}~. The color ~C_{d,i}~ is either Red, Blue, Yellow or Green, and ~n_{d,i}~ is an integer, where ~1 \leq n \leq 10^3~.

The last ~m~ lines contain ~C_{p,i}~ and ~n_{p,i}~, indicating that you have a card with color ~C_{p,i}~ and number ~n_{p,i}~. The color ~C_{p,i}~ is either Red, Blue, Yellow or Green, and ~n_{p,i}~ is an integer, where ~1 \leq n \leq 10^3~.

Output

Output the maximum number of cards that can be played in the game.

Clarifications

• The dealer or you can have multiple of the same card.
• You can only play ~1~ card at a time. Once played, it does not go back in your hand.
• Unlike Uno, "Wild Cards", "Skips" and "Reverses" do not exist.

Example

Input 1

3
Red 1
Yellow 3
Blue 5
Yellow 1
Yellow 5
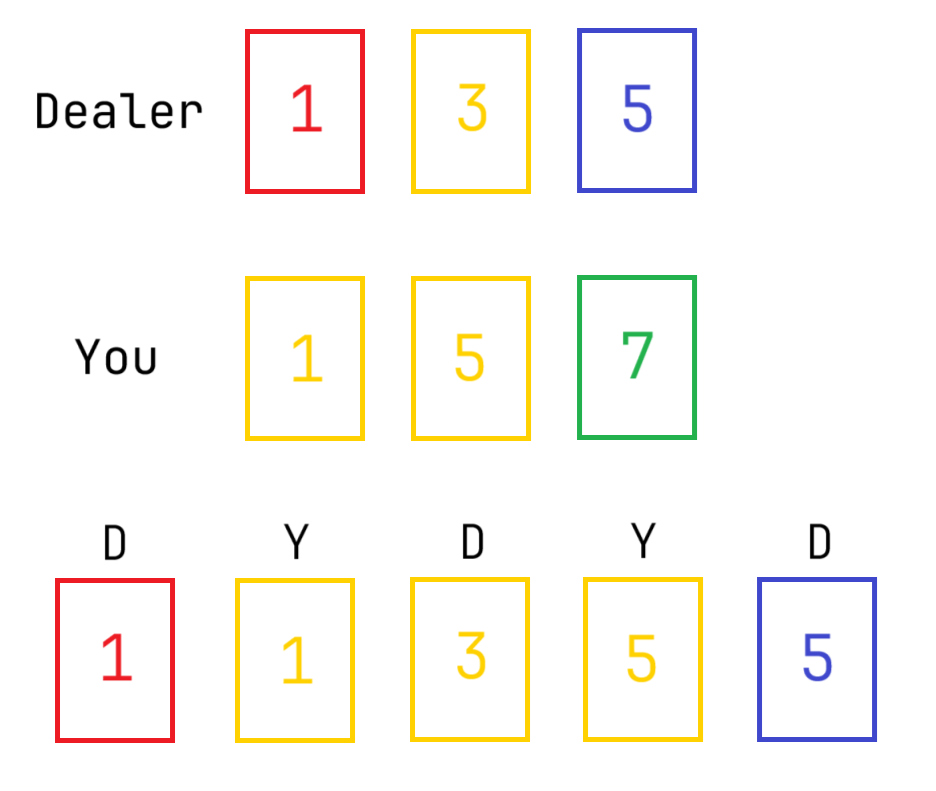
Green 7

Output 1

5

The longest game, with ~4~ cards played, could occur with the following series of moves:

• Dealer: Red ~1~
• You: Yellow ~1~
• Dealer: Yellow ~3~
• You: Yellow ~5~
• Dealer: Blue ~5~
• Game over, dealer wins.

Input 2

9
Red 1
Red 2
Red 3
Red 4
Red 5
Red 6
Red 7
Red 8
Red 9
Red 1
Red 2
Red 3
Red 4
Red 5
Red 6
Red 7
Red 8
Red 9

Output 2

18