After hearing the devastating news that the beloved sculptures of Rundle Mall were stolen, Tom wanted to give the people of Adelaide something special upon his return.

This gift would be a tower, meticulously crafted to fit the specifications that he has laid out. For ease of construction and transportation, this tower will be split into modules. These modules must be arranged and stacked in the correct order, otherwise it's not a valid Tower of Tom's!

Each module is denoted by a single character, and the rules for arranging them are as follows:

• o (sphere): There must be at least one in the tower.
• b (bird): There must be at least one in the tower, and it cannot be the first or the last.
• T (Tom's special): There must be one placed every ~3~ modules. That is, for a given module at index ~i~ (~1~-indexed), place one when ~i \equiv 0 \pmod{3}~.
• H (hat): If there is a hat, it must be at the top of the tower. There must be either ~0~ hats or ~1~ hat.

Tom tries to get some of his friends back home in Adelaide to rebuild it before he returns, but none of them can get it quite right! You can rearrange the modules of the existing tower by swapping them around, where moving a module by ~1~ position costs ~1~ unit of energy. Given the current configuration of the tower, determine the minimum total energy required to make it valid.

Input

The first line contains an integer ~n~ ~(1 \leq n \leq 100)~, the height of the tower.

The next line contains a string ~T~, the tower itself. The tower is laid on its side, with the start of the string representing the top of the tower.

Output

Output the minimum amount of energy required to make the tower valid.

Example

Input 1

7
oTHooTb

Output 1

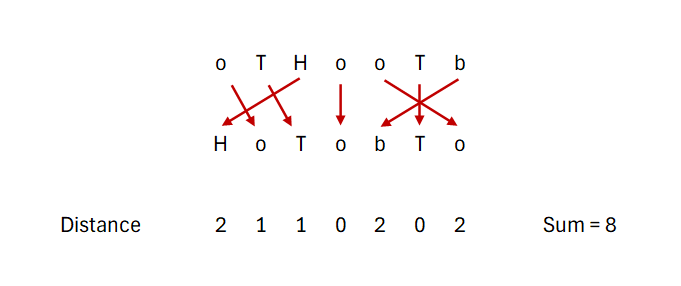
8

We can turn oTHooTb into HoTobTo, which is a valid Tower of Tom's, by the following operations:

• Move the o module on index 1 to index 2. Energy used = abs(1-2) = 1.
• Move the T module on index 2 to index 3. Energy used = abs(2-3) = 1.
• Move the H module on index 3 to index 1. Energy used = abs(3-1) = 2.
• Don't move the o module on index 4.
• Move the o module on index 5 to index 7. Energy used = abs(5-7) = 2.
• Don't move the T module on index 6.
• Move the b module on index 7 to index 5. Energy used = abs(7-5) = 2.

Input 2

6
ooTboT

Output 2

0

The tower is already in a valid state.

Input 3

6
booToH

Output 3

-1

The tower can never be brought into a valid state, as there aren't enough T modules to place one at every third index.