After some hooligans stole the Mall's Balls, you've been hired to rebuild them. Unfortunately, your construction crew may have slightly overestimated the number of balls required! Construction is already underway, so you'll just have to roll with it.

You have ~n~ identical circles, each with a diameter of ~100~ centimeters, and their horizontal (~x~) positions are fixed in a row. You may drop the circles in any order, one by one. When a circle is dropped:

• It falls straight down until it lands on the ground or touches any part of a previously dropped circle.
• If it touches another circle, it sticks and does not move further.
• Two circles stick together only when they are tangent (i.e., touch at exactly one point).

Your task is to determine the maximum possible height (vertical distance from the ground) that can be achieved at any point by carefully choosing the order in which to drop the circles.

Input

The first line consists of an integer ~n~ ~(1 \leq n \leq 10^5)~, the number of balls.

The next ~n~ lines consist of an integer ~x~ ~(1 \leq x \leq 10^8)~, indicating that there is a ball that must be dropped at ~x~ centimeters from the origin.

Output

Output the maximum height of the new sculpture you could build, in centimeters, correct to ~4~ decimal places.

Example

Input 1

3
200
150
200

Output 1

286.6025

There are ~3~ balls to stack:

• ~1~ at ~x = 150~
• ~2~ at ~x = 200~

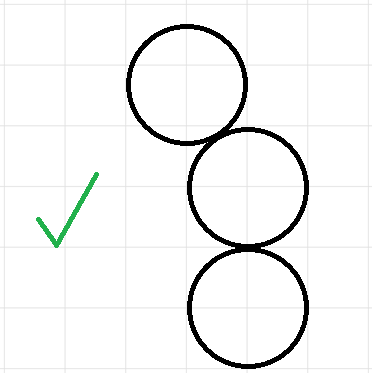
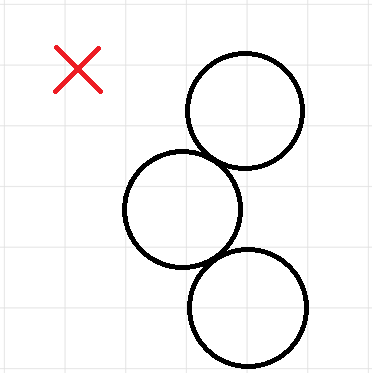
Input 2

5
500
280
300
410
540

Output 2

235.2405

Input 3

3
100
100
100

Output 3

300.0000