The Texas Sharpshooter Fallacy is a fallacy where someone takes meaningless data, and formulates patterns around it to pretend it holds some deeper meaning. A good analogy is shooting a blank wall, then painting a target around the bullet hole to pretend like you "got a bullseye".

After shooting the wall ~n~ times, you want to fool your friends into thinking you're a sharpshooter! If you draw a target of radius ~R~, what's the maximum number of bullets it could enclose?

Input

The first line contains two integers ~n~ and ~r~ ~(1 \leq n \leq 1000, 1 \leq r \leq 10^9)~, indicating that there are ~n~ bullet holes in the wall, and you will draw a target with a radius of ~r~ units.

The next ~n~ lines contain integers ~r~ and ~c~, ~(1 \leq r, c \leq 10^9)~, indicating that one of the bullet holes is ~r~ units above and ~c~ units to the right of the bottom-left corner of the wall. Each bullet hole has a unique position.

Output

Output the maximum number of bullet holes you could encapsulate in a target placed anywhere on the wall.

Clarifications

Bullets on the circumference of the target should be considered inside it.

Example

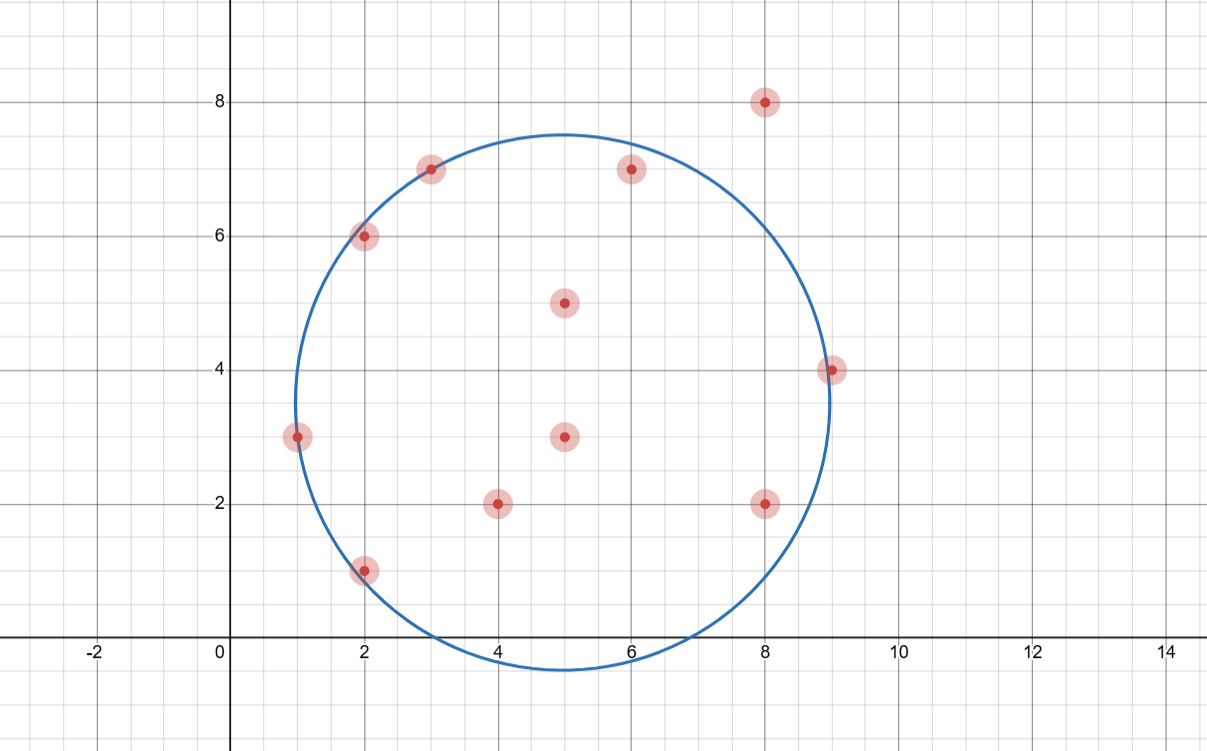
Input 1

11 4
1 3
8 2
6 7
2 6
4 2
8 8
5 3
3 7
9 4
5 5
2 1

Output 1

9

With a target of radius ~4~ centered at roughly ~(4.966479, 3.516760)~, you can capture 9 out of the 11 points. It can be shown that this is the maximum number of points you can capture.

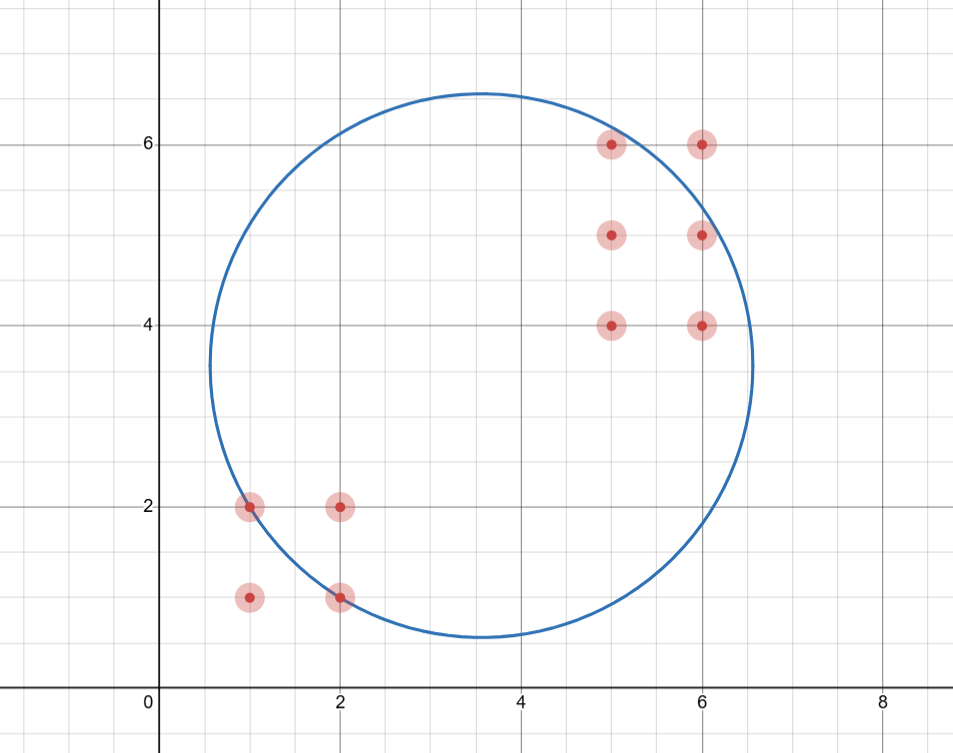
Input 2

10 3
1 1
1 2
2 1
2 2
5 5
5 6
5 4
6 5
6 6
6 4

Output 2

8

With a target of radius ~3~ centered at roughly ~(3.561553, 3.561553)~, you can draw a target that captures 8 out of the 10 points. It can be shown that this is the maximum number of points you can capture.

Input 3

5 1
0 0
0 1
1 0
0 2
1 1

Output 3

4