It's New Years 2067, and Axel needs to get from his house to the Sydney Harbour Bridge. The city can be modelled as a collection of ~n~ interchanges, numbered from ~1~ to ~n~. These interchanges are joined by various types of public transport, and there are ~m~ connections in total.

Axel's house is at interchange ~1~, and he wants to get to the Harbour Bridge at interchange ~n~ by travelling along the connections. He doesn't want to visit the same interchange more than once, and only wants to use a single form of public transport for the whole trip (i.e. only taking the Train).

How many ways can he get from interchange ~1~ to interchange ~n~, using each type of transport available?

Input

The first line contains two integers ~n~ and ~m~ (~1 \leq n \leq 10~, ~1 \leq m \leq 1000~), the number of interchanges in Sydney, and the number of connections between them.

The next ~m~ lines contain two integers ~a~ and ~b~ ~(1 \leq a, b \leq n)~ and an uppercase string ~S~ ~(1 \leq |S| \leq 10)~, indicating that Axel can travel from interchange ~a~ to ~b~ using the public transport ~S~. There are at most ~1000~ unique transport types. These lines are guaranteed to be unique.

Output

Output the number of ways to travel from interchange ~1~ to interchange ~n~ using only one type of public transport, listed in alphabetical order by transport type.

Example

Input 1

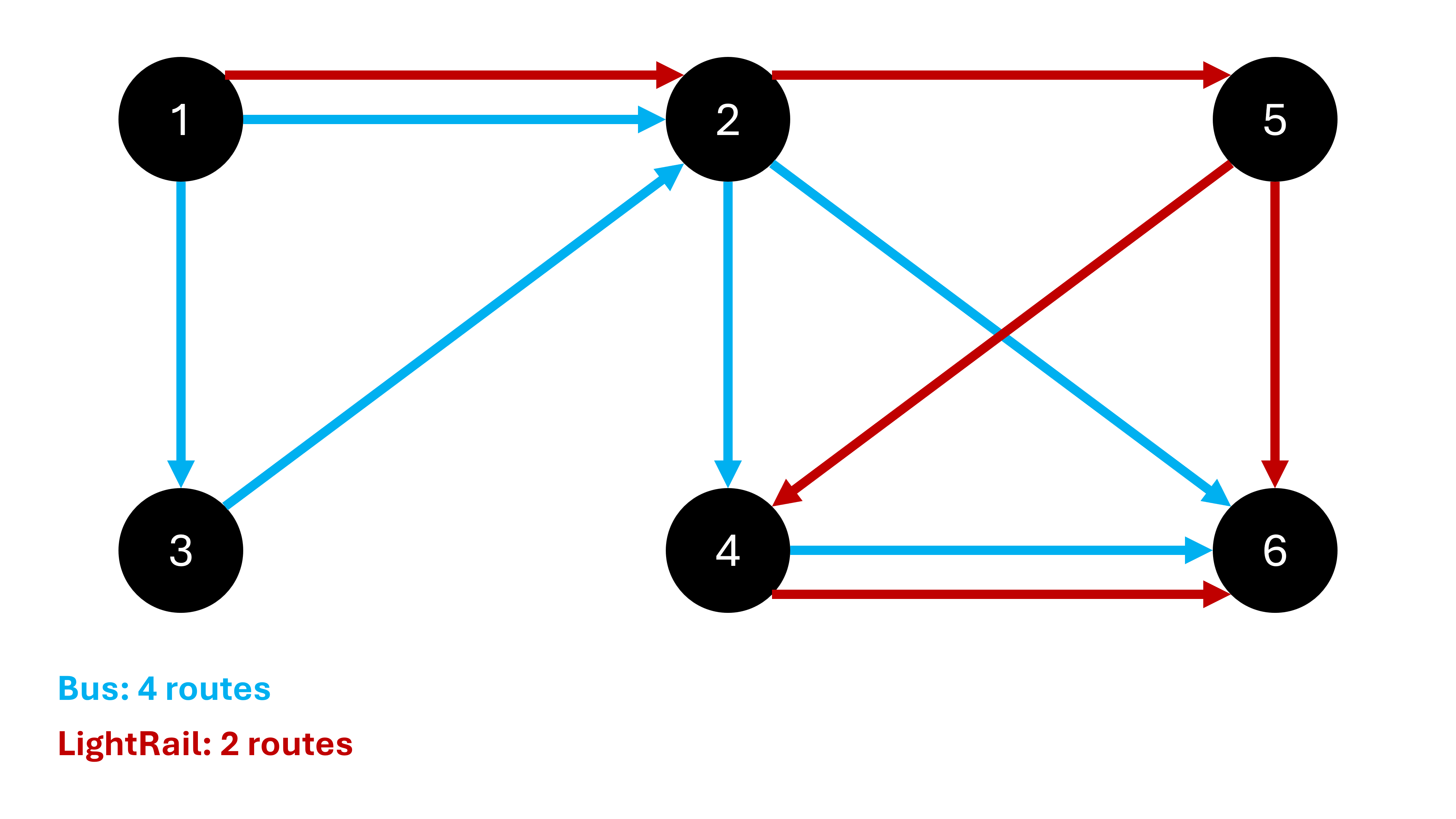
6 11
1 2 BUS
1 2 LIGHTRAIL
1 3 BUS
3 2 BUS
2 4 BUS
2 5 LIGHTRAIL
2 6 BUS
5 4 LIGHTRAIL
5 6 LIGHTRAIL
4 6 BUS
4 6 LIGHTRAIL

Output 1

BUS 4
LIGHTRAIL 2

There are ~4~ ways to get from interchange ~1~ to ~6~ via bus:

• 1 -> 2 -> 6
• 1 -> 2 -> 4 -> 6
• 1 -> 3 -> 2 -> 6
• 1 -> 3 -> 2 -> 4 -> 6

There are ~2~ ways to get from interchange ~1~ to ~6~ via lightrail:

• 1 -> 5 -> 6
• 1 -> 5 -> 4 -> 6

Input 2

4 12
1 2 TRAIN
2 4 TRAIN
1 3 TRAIN
3 4 TRAIN
1 2 FERRY
2 4 FERRY
1 3 FERRY
3 4 FERRY
1 4 FERRY
2 3 FERRY
3 2 FERRY
4 1 FERRY

Output 2

FERRY 5
TRAIN 2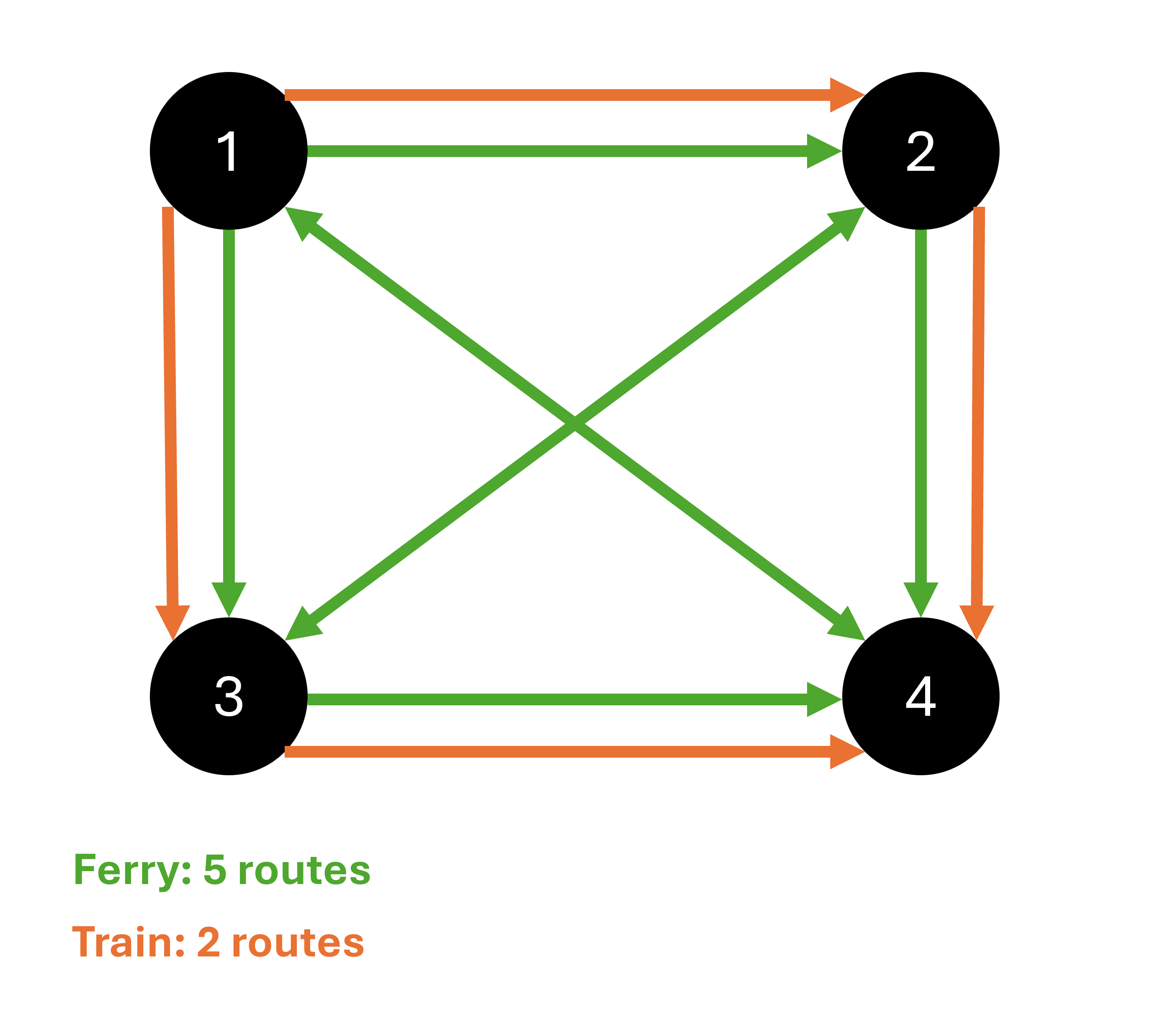

Input 3

3 2
1 2 METRO
2 3 WALK

Output 3

METRO 0
WALK 0