Rob and his cronies have arrived from interstate with an evil plan to deprive Adelaideans of their beloved icons. Of course, we're talking about the sculptures and statues in Rundle Mall. They want to steal a sculpture each night, working their way to the final night where they steal the crown jewels of Adelaide: The Mall's Balls.

Rob is tired of hearing Adelaideans rave about how good their pigs and Mall's Balls are, and wants to put and end to it once and for all! After this heist, Adelaide will become less recognisable and memorable — just as he intends.

Rob and his enterprising criminal buddies are not stupid, however. They know that to pull off a successful heist night after night, they need to beware of things that could get them caught. From security cameras and roadworks, to even traffic light patterns — anything that slows them down or gets in their way will only worsen their chances of a successful heist.

Rob's right-hand man is Bert, and he is tasked with calculating the escape route they should take to minimise their chances of being caught. Bert labels each intersection and road with some risk ~r~ of getting caught, based on numerous factors. He can minimise the chances of getting caught by taking a route with the lowest total risk factor. Can Bert find an ideal getaway route for each night, or will Rob's spree come to an abrupt end?

Input

The first line consists of integers ~n~ and ~m~ — where ~n~ ~(2 \leq n \leq 10^5)~ is the number of intersections, and ~m~ ~(1 \leq m \leq 10^5)~ is the number of roads that are connected by two intersections.

The next ~n~ lines contain a string ~I~ and a risk factor ~r~ ~(1 \leq r \leq 10^5)~ of getting caught at that intersection.

The next ~m~ lines contain three strings ~N~, ~I_A~, and ~I_B~, and a risk factor ~r~. This means that there is a road with the name ~N~ that connects two intersections ~I_A~ and ~I_B~.

The final line of the input contains two strings ~I_1~ and ~I_2~, representing the intersection you start from and the intersection you want to end up on, respectively.

All of the strings are alphanumeric, contain no spaces, and have a length between ~1~ and ~10^3~ inclusive.

Output

Output the lowest total risk factor if you take the getaway route that will minimise your chances of being caught. You should also output the total number of risks taken, which is the number of intersections and roads you have gone through.

Clarifications

• You will never start and end at the same intersection.

Example

Input 1

6 7
PSRS 10
FSRS 10
ETRS 10
PSGS 10
FSGS 10
ETGS 10
RundleStreet PSRS FSRS 90
RundleStreet FSRS ETRS 90
PultneyStreet PSRS PSGS 80
FromeStreet FSRS FSGS 70
EastTerrace ETRS ETGS 50
GrenfellStreet PSGS FSGS 70
GrenfellStreet FSGS ETGS 70
PSRS ETGS

Output 1

260 7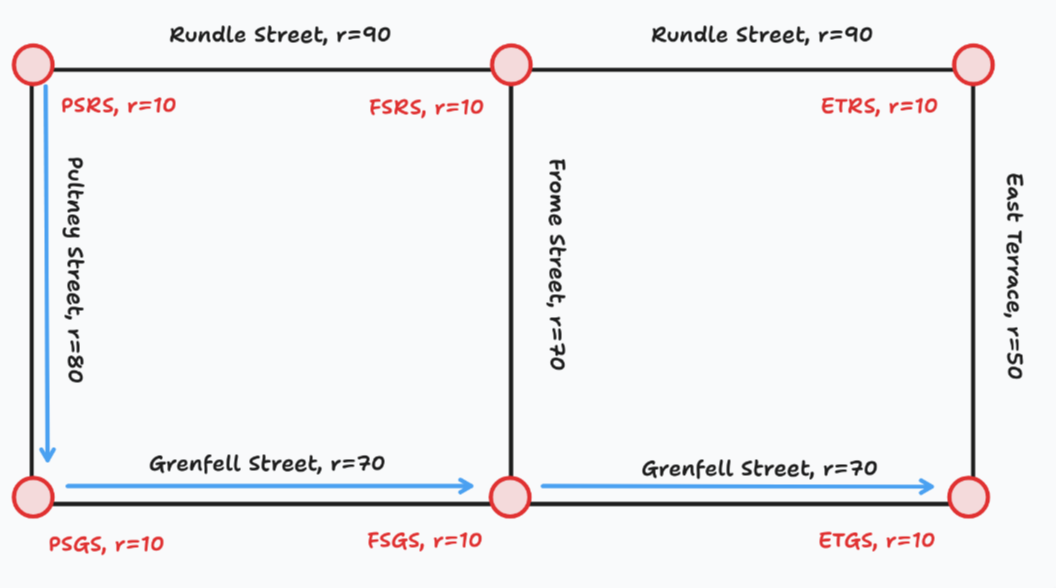

The goal is to get from PSRS (the Pultney Street and Rundle Street intersection) to ETGS (The East Terrace and Grenfell Street intersection). The getaway route that minimises the total risk factor is highlighted by the blue arrows, and can be calculated as follows:

~10 + 80 + 10 + 70 + 10 + 70 + 10 = 260~

We also output the number of intersections and roads we have gone through, which is ~7~.