Rory and Tony were getting bored doing LeetCodes after solving 4 consecutive medium questions, so they decided to go to a nearby mini-golf course in the city. At this mini-golf course, the course is a two-dimensional plane with a bunch of bumpers of some fixed radius centred at distinct coordinates.

In the game, a ball is always hit from the tee at coordinates ~(0,0)~ with some angle ~0\leq \theta< 360~ counted counter-clockwise from the positive ~x~-axis. Rory wants to know for a bunch of different potential shots which of them will hit a bumper eventually and which will go off into the distance forever. If they will hit a bumper eventually, Rory wants to know how far the ball will have travelled before hitting the bumper. Can you help him out so he can finally beat Tony in this game of putt-putt golf.

Input

The first line consists of two integers ~n~ ~(1\leq n\leq 10^5)~ and ~r~ ~(1\leq r \leq 1000)~, the number of bumpers and the radius of each of the bumpers.

The next ~n~ lines each contain two space-separated integers ~x_i~ and ~y_i~ ~(-10^6 \leq x_i,y_i \leq 10^6)~, the position of the centre of each of the bumpers. It is guaranteed that none of the bumpers intersect the origin.

The next line contains a single integer ~q\ (1 \leq q \leq 10^5)~, the number of different shots that Rory wants to try.

The next ~q~ lines each contain a single integer ~\theta_i\ (0 \leq \theta_i < 360)~, the angle of the ~i~th shot counter-clockwise from the positive ~x~-axis.

Output

For each of the ~q~ shots, output if it will hit or miss a bumper.

If it will hit a bumper, output 'HIT' on a line, along with the distance the ball will have travelled before it hits the first bumper. This distance should be rounded to a ~4~ decimal places.

If it will hit no bumpers, output 'MISS'.

Clarifications

Shots that are tangent to a bumper count as a hit.

Example

Input 1

3 1
3 0
2 2
5 -2
4
0
45
330
90

Output 1

HIT 2.0000
HIT 1.8284
HIT 4.6896
MISS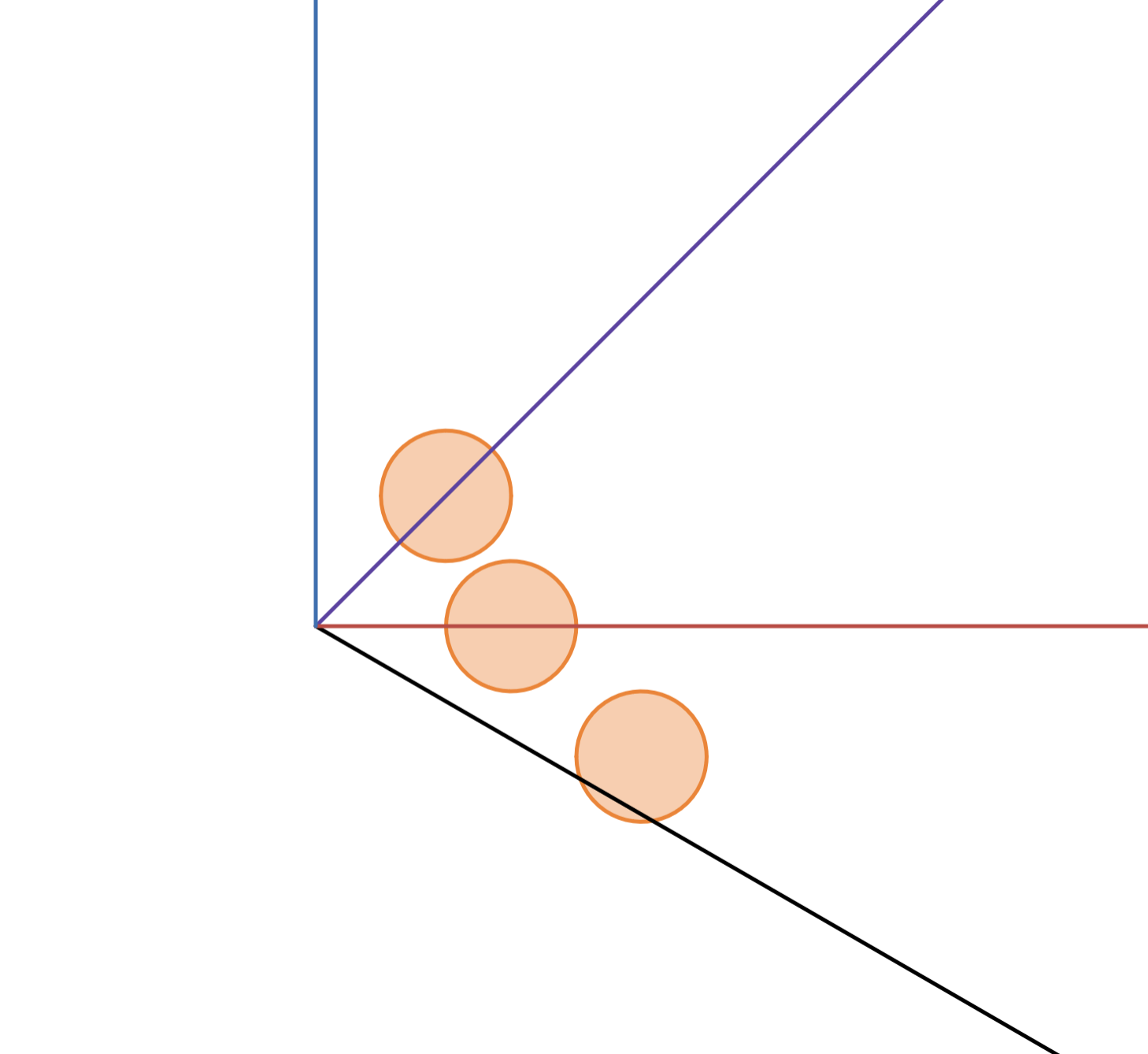

The case is shown above. The first shot is red, the second shot is purple, the third shot is black, the fourth shot is blue.

The first shot will intersect the bumper centred at ~(3,0)~. Since it has a radius of ~1~, the intersection point is ~(2,0)~ which is a distance of ~2~ from the origin along the line of travel.

The second shot will intersect the centre of the bumper at ~(2,2)~. The distance travelled can be calculated to be ~\sqrt{8}-1\approx 1.828~.

The third shot will intersect the lower half of the bumper at ~(5,-2)~, having travelled a distance of approximately ~4.690~.

The final shot will travel straight in the ~+y~ direction, which has no bumper covering it.

Input 2

3 2
4 -2
0 10
-5 -5
3
45
225
0

Output 2

MISS
HIT 5.0711
HIT 4.0000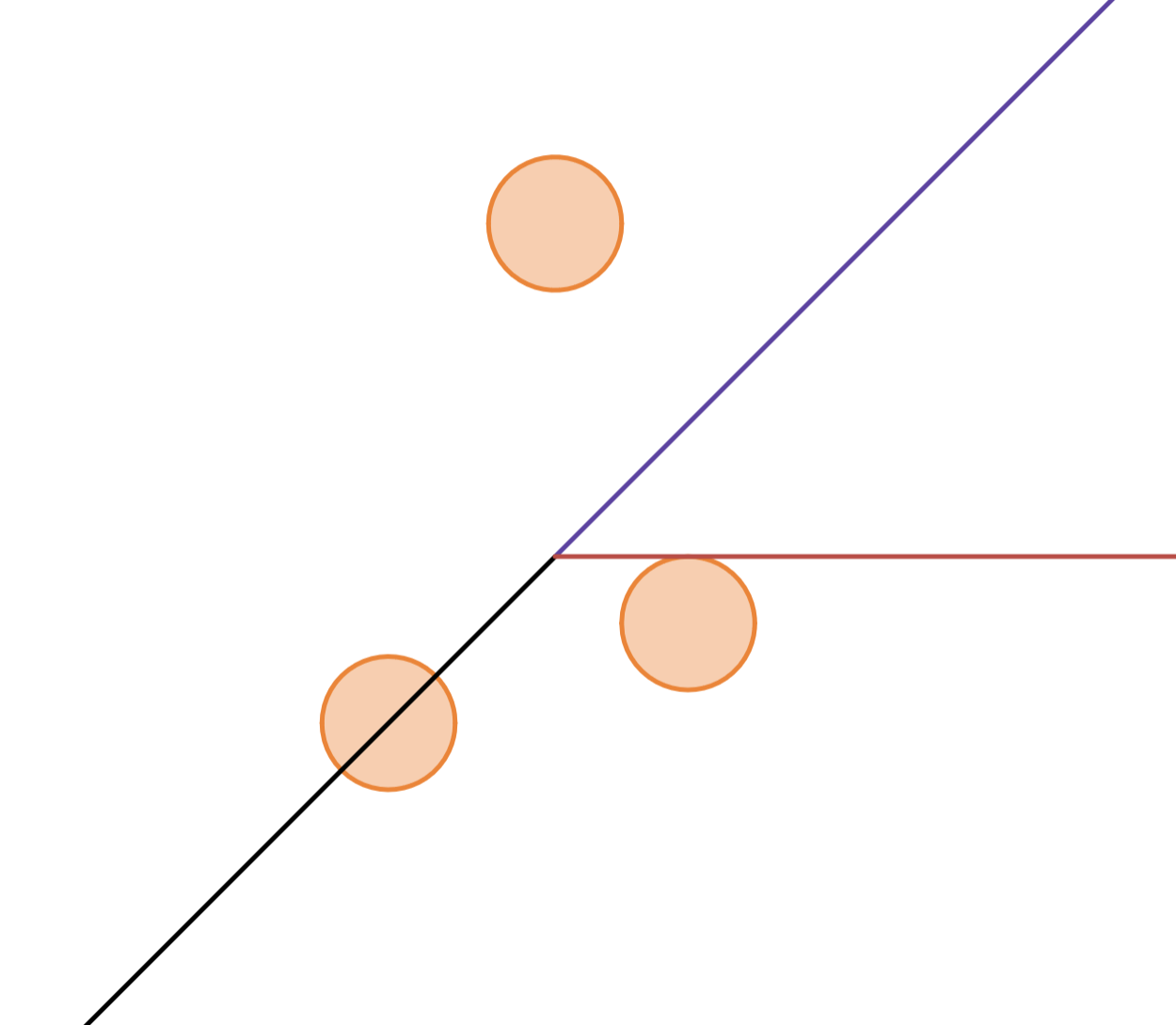

The case is shown above. Note you see tangents count as a hit here.