Some people plot to take over the world. Farmer Ray plots flowers.

Ray has an ~n \times m~ plot of land he'd like to place flower beds in. He has two kinds of flower beds:

• Long beds, which are ~n \times 1~.
• Tiny beds, which are ~1 \times 1~.

Ray can arrange any number of these beds within his plot so that they don't overlap, completely cover the plot, and don't go outside of it. How many arrangements of beds can he make?

Input

The only line contains two integers ~n~ ~(1 \leq n \leq 10^5)~ and ~m~ ~(1 \leq m \leq 15)~, the dimensions of Ray's plot.

Output

Output the number of ways Ray can fill out his flowerbed using any number of ~1 \times n~ and ~1 \times 1~ flower beds.

Clarifications

• Rotations of the same arrangement are considered different to each other.
• An arragement can use all of the same type of bed. There is no limit to the number of beds that Ray has.

Example

Input 1

3 4

Output 1

56

There are 56 possible arrangements of ~3 \times 1~ and ~1 \times 1~ flowerbeds on a ~3 \times 4~ plot of land.

Input 2

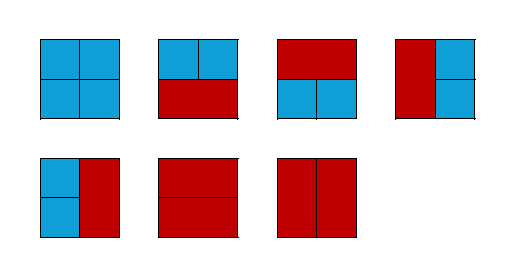
2 2

Output 2

7

There are 7 possible arrangements of ~2 \times 1~ and ~1 \times 1~ flowerbeds on a ~2 \times 2~ plot of land.

Input 3

1 1

Output 3

2

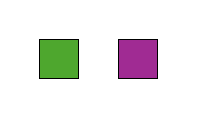
In this case, the plots are ~1 \times 1~ or ~1 \times 1~. In this edge case, we consider the types of plots to be distinct, so there are 2 arrangements.