Adelaide has a vast and complex plumbing network.

There are ~n~ houses, with ~m~ pipes flowing between them. Each pipe has some capacity, in liters.

Consider a path of pipes between two houses. The "flow" of that path is the minimum capacity along that path (or, it's "bottleneck").

Now, consider all paths between two houses. The "widest flow" is equal to the path with the biggest flow.

For example, consider this network of pipes:

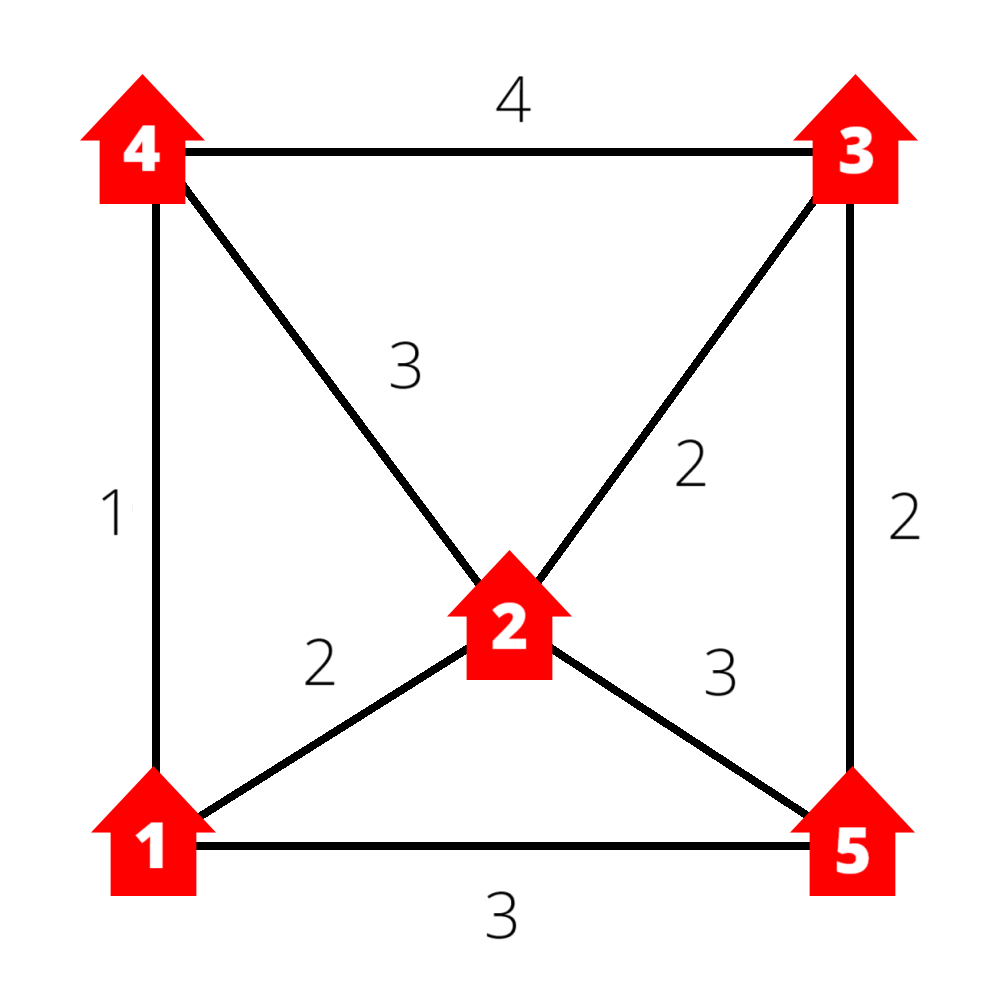
The "widest flow" between house ~1~ and house ~3~ is ~3~. This path goes from house ~1 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 3~, and has a flow of ~3~, since its smallest pipe and hold 3 liters.

There are several other paths between house ~1~ and house ~3~, but they don't have the widest flow. For example:

• ~1 \rightarrow 2 \rightarrow 3~, with a flow of ~2~.
• ~1 \rightarrow 4 \rightarrow 3~, with a flow of ~1~.

Today, you have gotten ~q~ phone calls, asking you what the widest flow is between two houses. Answer them!

Input

The first line consists of an integer ~n~ ~(1 \leq n \leq 100)~, the number of houses in the plumbing network.

The second line consists of an integer ~m~ ~(1 \leq m \leq 10^4)~, the number of pipes in the plumbing network.

The next ~m~ lines are in the form ~a \; b \; w~, signifying that there is a pipe of capacity ~w~ ~(1 \leq w \leq 10^8)~ between houses ~a~ and ~b~.

The next line consists of an integer ~q~ ~(1 \leq q \leq 10^5)~, the number of queries for you to answer.

The next ~q~ lines are in the form ~a \; b~, meaning you need to output the "widest flow" between houses ~a~ and ~b~.

Note: Each pair of houses may have at most 1 pipe between them.

Output

Output the maximum "widest flow" for each query.

Note: The graph is not guaranteed to be connected. If two houses are completely disconnected, their "widest flow" is -1.

Example

Input

5
8
1 2 3
1 4 1
1 5 3
2 3 2
2 4 3
2 5 3
3 4 4
3 5 2
3
1 3
2 3
3 4

Output

3
3
4

This is the above example.

• We have established that the widest flow from house ~1~ to house ~3~ is ~3~.
• The widest flow from house ~2~ to house ~3~ is ~3~. The optimal path is ~2 \rightarrow 4 \rightarrow 3~.
• The widest flow from house ~3~ to house ~4~ is ~4~. The optimal path is ~3 \rightarrow 4~.

Input

5
4
1 2 1
2 3 1
3 4 1
4 5 1
4
1 3
2 3
3 4
1 4

Output

1
1
1
1