Ilias the hard-working chicken farmer has just acquired a flock of quadrangle chickens, and he needs to build a pen for them. He has an infinite field of land with ~n~ available positions for the corners of the pen.

However, Ilias's chickens are picky: they'll only live in a pen that satisfies the following conditions:

• The pen is an enclosed parallelogram.
• The pen is not a square or rectangle.
• The pen has a non-zero area.

How many distinct pens can Ilias build that meet the chickens' requirements?

Input

The first line contains one integer, ~n~, ~(1 \leq n \leq 800)~ the number of potential positions for the corners of the pen.

The next ~n~ lines contain two integers ~x_i~ and ~y_i~ ~(0 \leq x_i, y_i \leq 10^5)~, indicating that a corner of the pen can be placed at position ~(x_i, y_i)~.

The points given are guaranteed to be unique.

Output

Output the number of distinct strictly parallelogram pens Ilias can create from the available corner positions.

Example

Input 1

8
1 1
1 3
2 2
3 5
4 1
4 3
6 2
6 5

Output 1

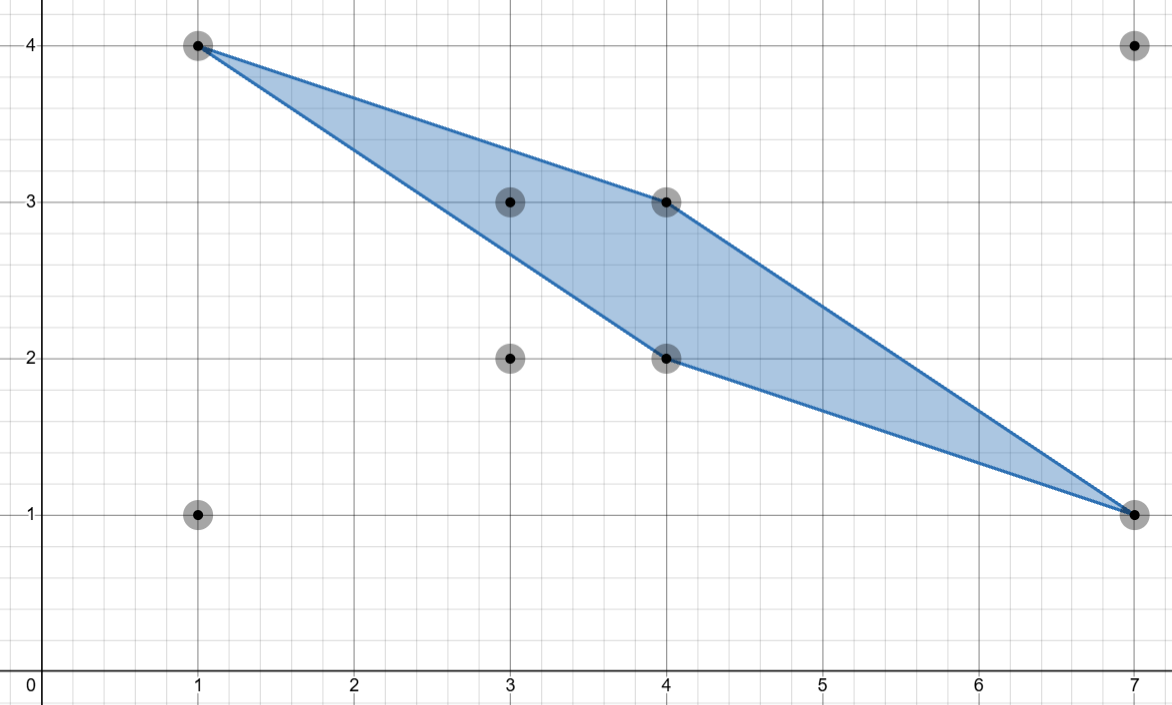
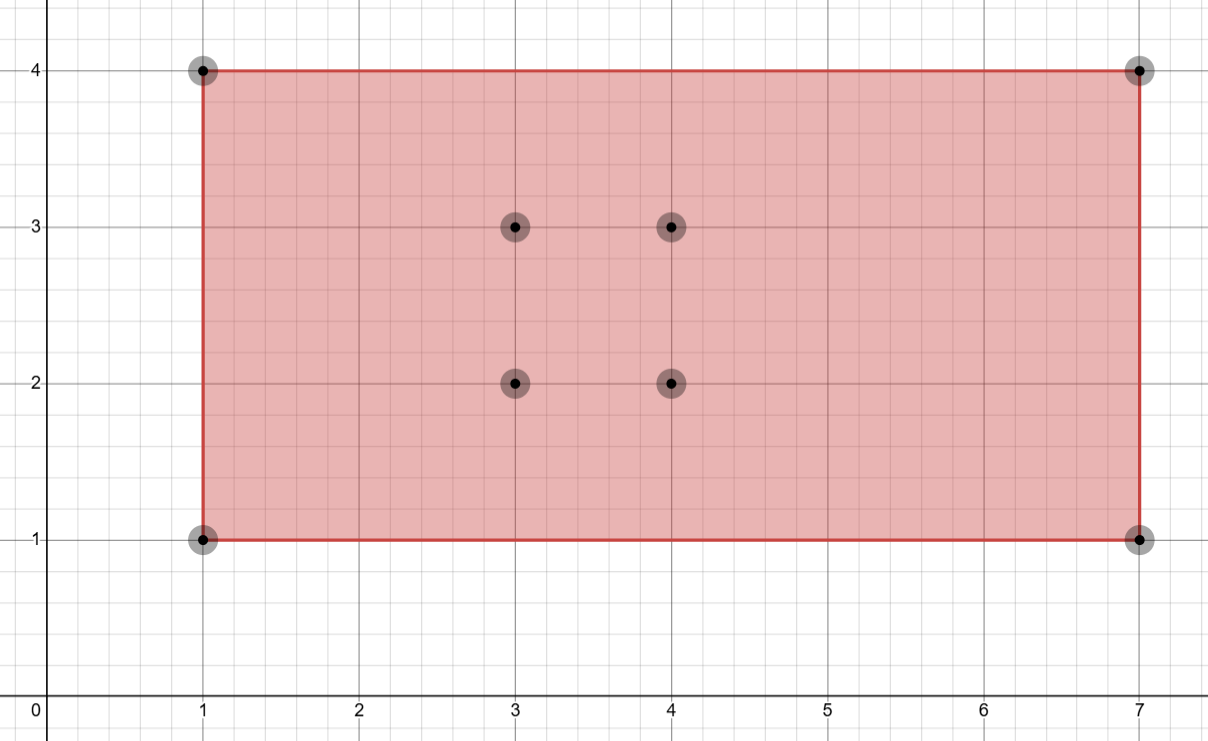
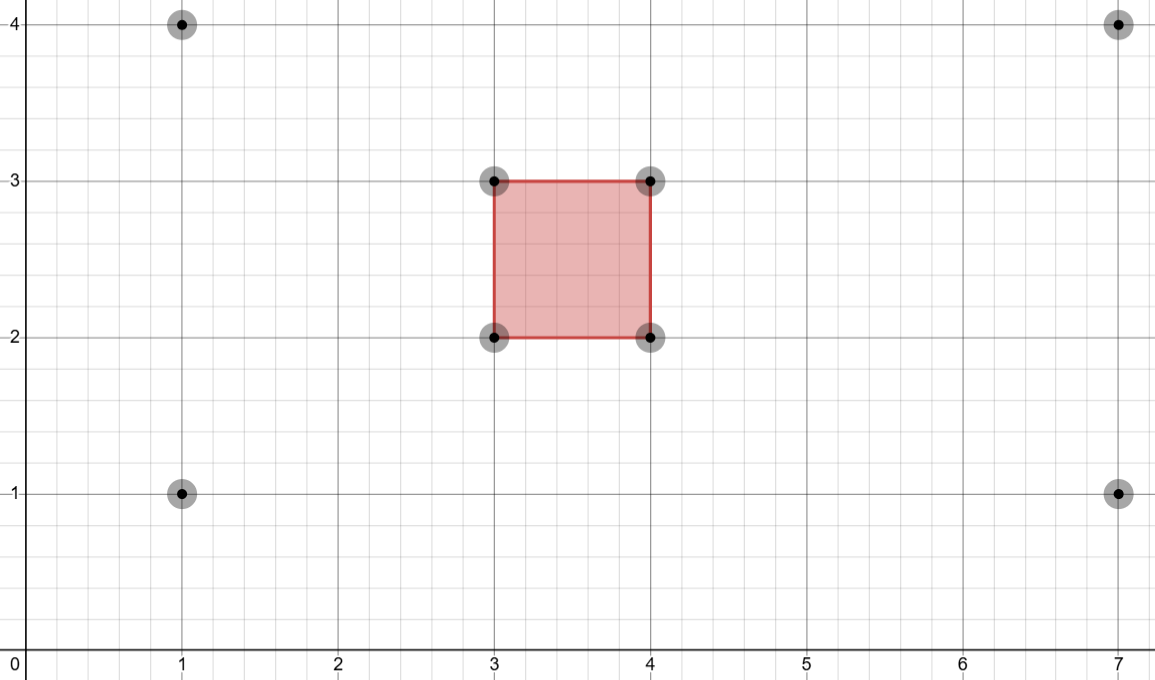
3

There are ~4~ total parallelograms that can be formed from the points. Of these, three are valid (blue) and one is invalid (red).

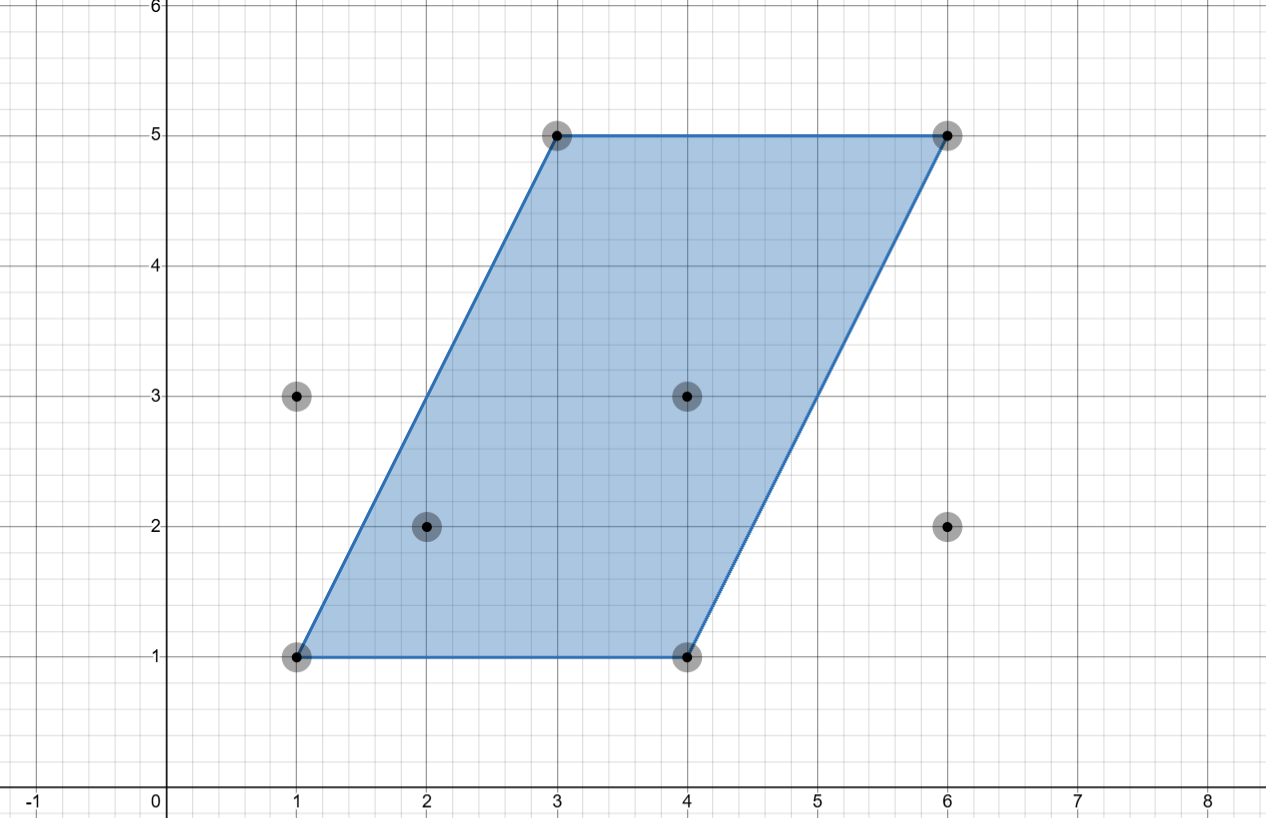
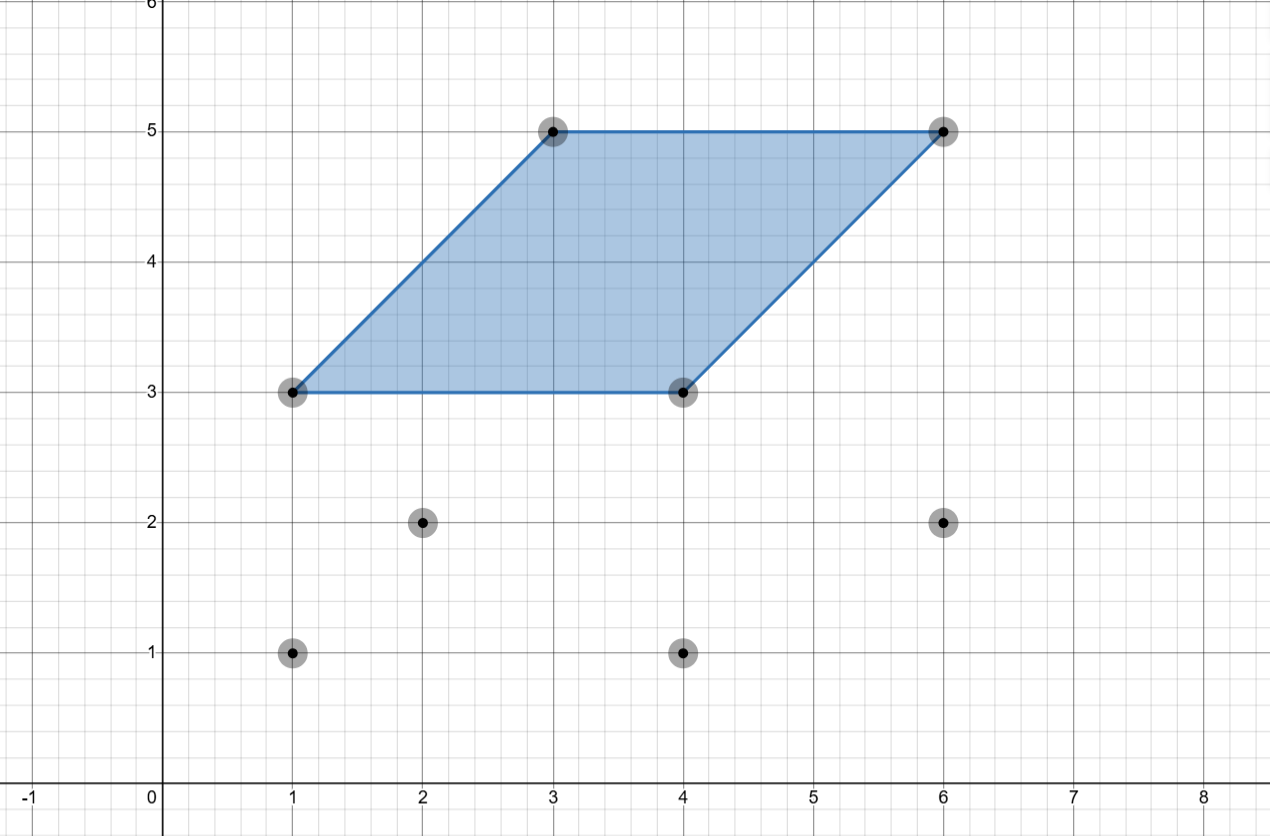
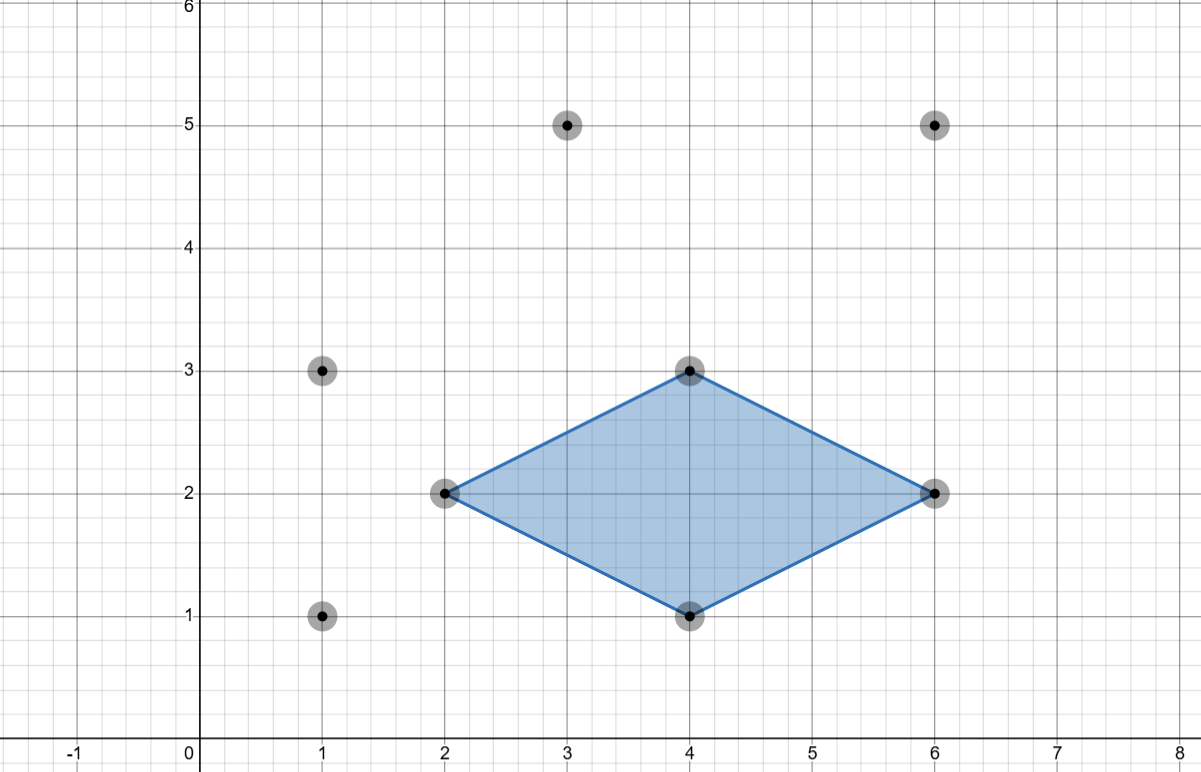
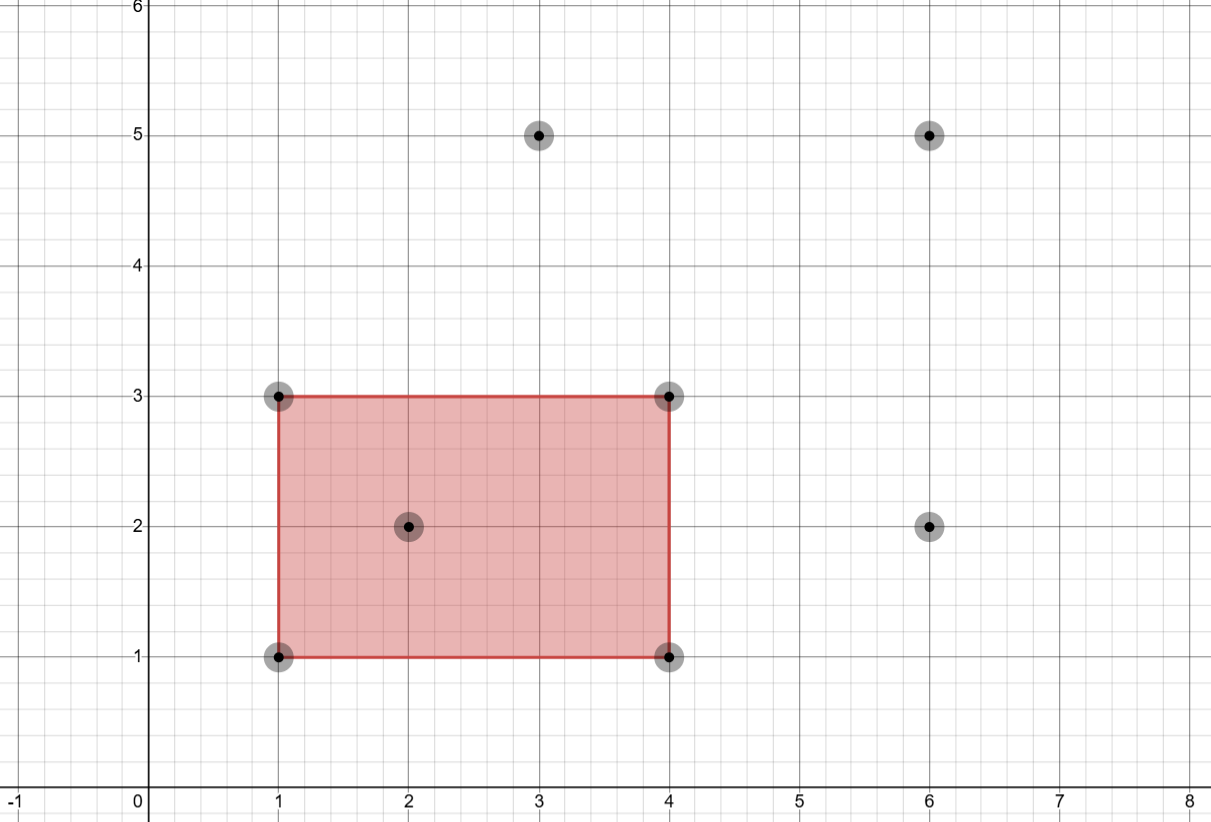
Input 2

8
3 2
3 3
4 3
4 2
1 1
1 4
7 4
7 1

Output 2

2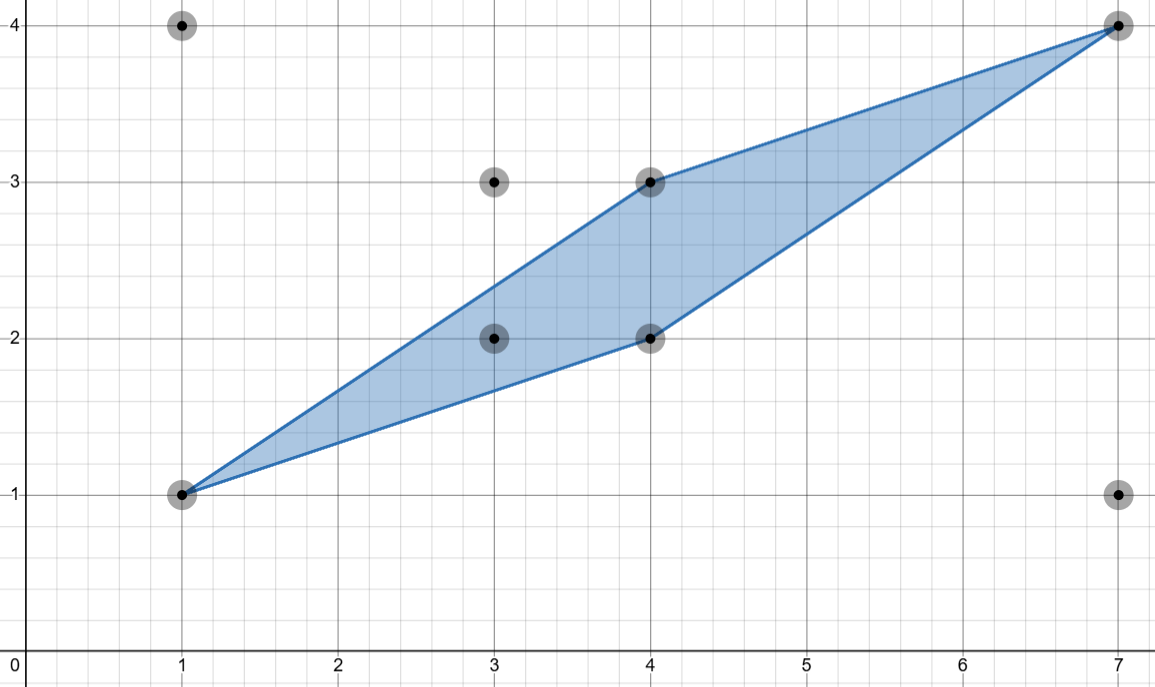

Input 3

8
1 1
1 2
2 1
2 2
3 5
3 6
4 5
4 6

Output 3

10