Rory is travelling from Adelaide to Mildura for the holidays, but he doesn't particularly like Mildura.

As such, he would like to travel as slowly as possible, making stops along the way. To do so, he will find places where he can plausibly stall his journey, such as stopping in a town with a tyre shop along to the way because his car "broke down", or a popular tourist destination because "it was on the way and he had to go see it". At different destinations, he will be able to stall for different amounts of time.

Unfortunately, Rory knows that if he stops more than three times, his family will get suspicious.

Given all of the stall destinations and all of the roads, can you find the longest amount of time he can stall for, making sure his family doesn't get suspicious?

Input

The first line consists of a single integer ~n~ ~(2 \leq n \leq 10^{5})~, the number of towns that may be passed through.

The next ~n~ lines each consist of a string ~T_i~, a given destination's name, and an integer ~s_i~ ~(0 \leq s_i \leq 10^{5})~, how long he can stall at for this particular location. All inputs will contain the following:

adelaide 0
mildura 0

The next line consists of a single integer ~m~ ~(1 \leq 10^{5})~, the number of roads between these towns.

The next ~m~ lines are of the format ~u_i~ ~v_i~, the names of two towns. This indicates that there is a directed road from town ~u_i~ to ~v_i~.

There is guaranteed to be no cycles in the road network, where all towns are reachable starting from adelaide, and all roads eventually lead to mildura.

Output

Output a single integer, the maximum amount of time Rory can stall for by stopping at no more than three towns on the way from adelaide to mildura.

Clarifications

• All town names only consist of uppercase letters, lowercase letters, and numbers, and are between ~1~ and ~100~ characters long, inclusive.
• There will be no duplicated roads between any two towns, cycles, or unconnected components.
• Rory can stop less than ~3~ times on the way from Adelaide to Mildura if he likes.

Examples

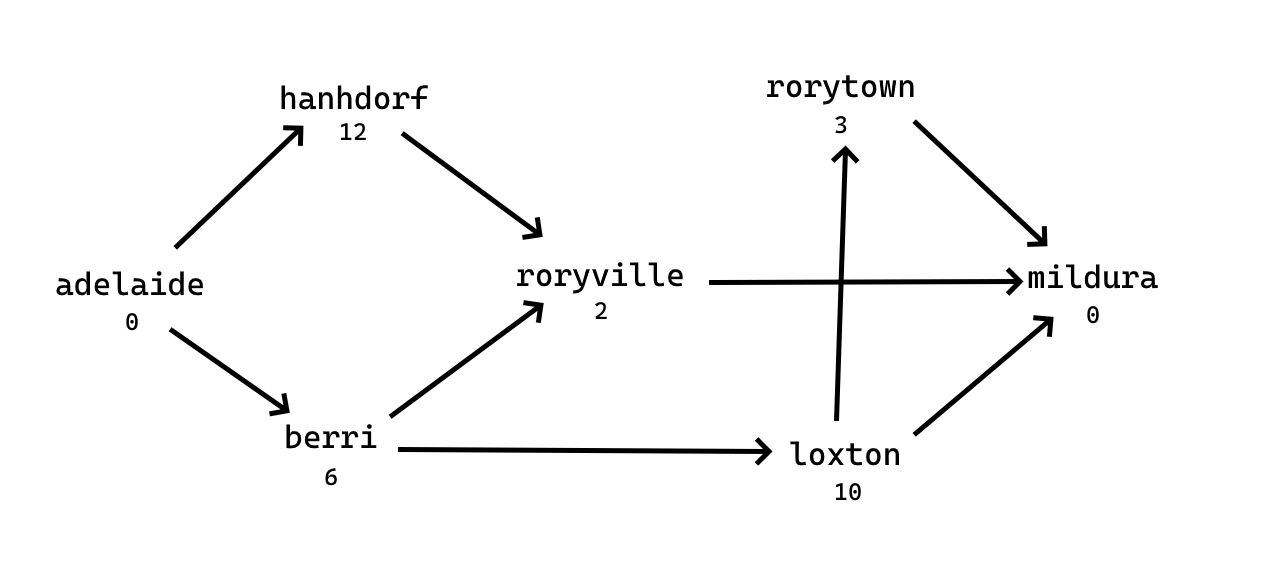
Input 1

7
adelaide 0
mildura 0
hanhdorf 12
berri 6
loxton 10
rorytown 3
roryville 2
9
adelaide hanhdorf
adelaide berri
berri loxton
berri roryville
hanhdorf roryville
loxton rorytown
loxton mildura
rorytown mildura
roryville mildura

Output 1

19

Explanation

Rory can stall for the longest amount of time by going from adelaide -> berri -> loxton -> rorytown -> mildura, stalling in berri, loxton, and rorytown for a total time of ~19~.