After the first round of the ICMT State Final Math Championships, Marymount and North Shore High are tied. Now, Cady's competing in a sudden death round for the win. The question appears above her.

"In what places do these two polynomials intersect?"

There's no time to waste! Solve this question and bring home the title!

Input

The first line consists of an integer ~n~ ~(0 \leq n \leq 10)~, the degree of the first polynomial.

The second line consists of integers ~a_{n}, a_{n-1}, ..., a_{1}, a_{0}~ ~(-10 \leq a_{i} \leq 10)~, describing the first polynomial's coefficients. There are exactly ~n+1~ coefficients.

The third line consists of an integer ~m~ ~(0 \leq m \leq 10)~, the degree of the second polynomial.

The last line consists of integers ~b_{m}, b_{m-1}, ..., b_{1}, b_{0}~ ~(-10 \leq b_{i} \leq 10)~, describing the second polynomial's coefficients. There are exactly ~m+1~ coefficients.

The equations for the two polynomials are:

• ~f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + ... + a_{1}x + a_{0}~
• ~g(x) = b_{m}x^{m} + b_{m-1}x^{m-1} + ... + b_{1}x + b_{0}~

Output

Output all the places where the two polynomials intersect, in ascending order of ~x~, to ~4~ decimal places.

Clarifications

• The coefficients of the polynomials are all integers.
• The polynomials will intersect at least once and no more than ~10~ times.
• Each number in your answer should be correct to ~4~ decimal places.

Example

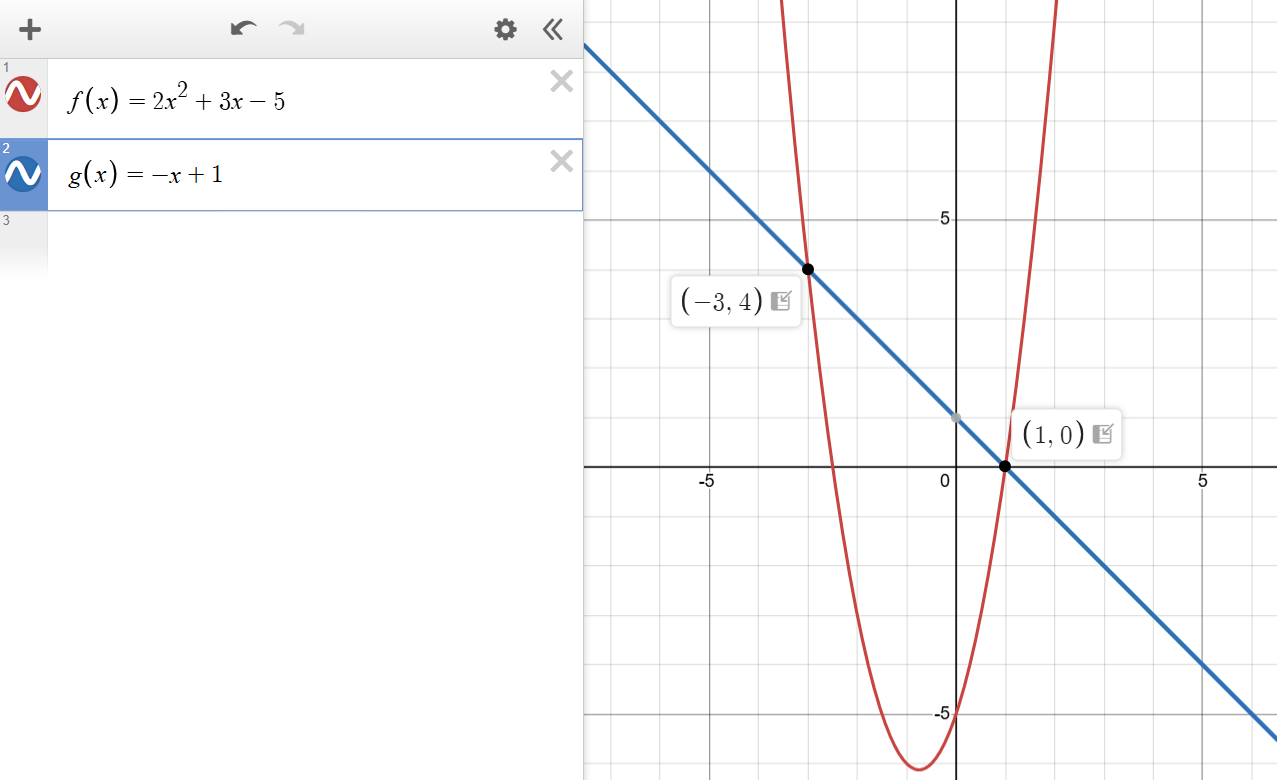
Input

2
2 3 -5
1
-1 1

Output

-3.0000 4.0000
1.0000 0.0000

These polynomials intersect twice.

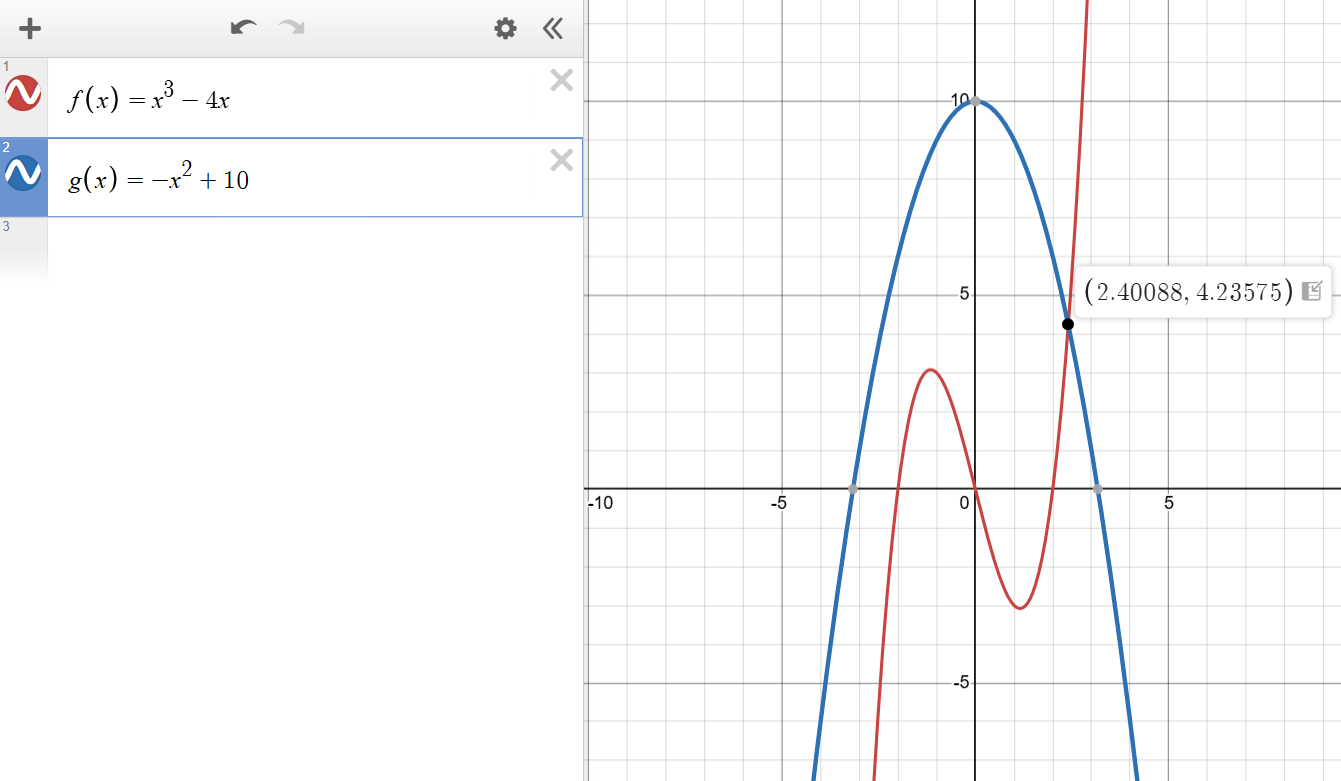
Input

3
1 0 -4 0
2 
-1 0 10

Output

2.4009 4.2358

These polynomials intersect once.