After a long day of market making, James decides to go outside. However, the layout of his neighbourhood has always confused him, and he is interested in studying a specific property of the streets within it. The neighbourhood consists of ~n~ intersections labelled ~1~ through ~n~, and ~n-1~ two-way roads connecting them, forming a tree structure.

Additionally, each street has a sign with an integer ~t_i~ on it. James loves streets, but he also loves palindromes. When he walks on a path between two intersections, he writes down the value he sees on the sign of each street he passes through on the way. He calls the path balanced if he can rearrange the values written into a palindrome — that is, each of them besides possibly one appears an even amount of times on the path. The palindrome is in terms of the numbers themselves as units, not digit-wise.

The tree of intersections and streets is rooted at James' house, located on intersection ~1~. For each intersection ~i~, James wants to find the number of distinct pairs of intersections ~(x,y)~ in the subtree of ~i~ (including ~i~) such that the path between ~(x,y)~ is balanced. If ~(x,y)~ counts, then ~(y,x)~ does not count.

Input

The first line contains a single integer ~n~ ~(1 \leq n \leq 10^5)~, the number of intersections in James' neighbourhood.

The next ~n-1~ lines each contain the details of a bidirectional road, which are ~u~, ~v~, and ~t~ ~(1 \leq u,v \leq n, u\neq v,1 \leq t \leq 20)~, where ~u~ and ~v~ are the intersections connected by a street and ~t~ is the value of the sign on that street. It is guaranteed that the intersections together with the roads connecting them form a valid tree.

Output

Output ~n~ integers on a single line, where the ~i~th integer represents the number of distinct unordered pairs of intersections in the subtree of the ~i~th intersection with a valid balanced path between them.

Clarifications

• Each path must refer to the unique simple tree path between two intersections ~i~ and ~j~. You cannot visit a node twice, or do any other loops.
• You cannot start and end at the same intersection (i.e., an empty path is not a valid balanced path). However, all one-length paths (and many other types) are balanced.

Example

Input 1

6
1 2 2
2 3 2
2 4 1
1 5 1
5 6 1

Output 1

11 2 0 0 1 0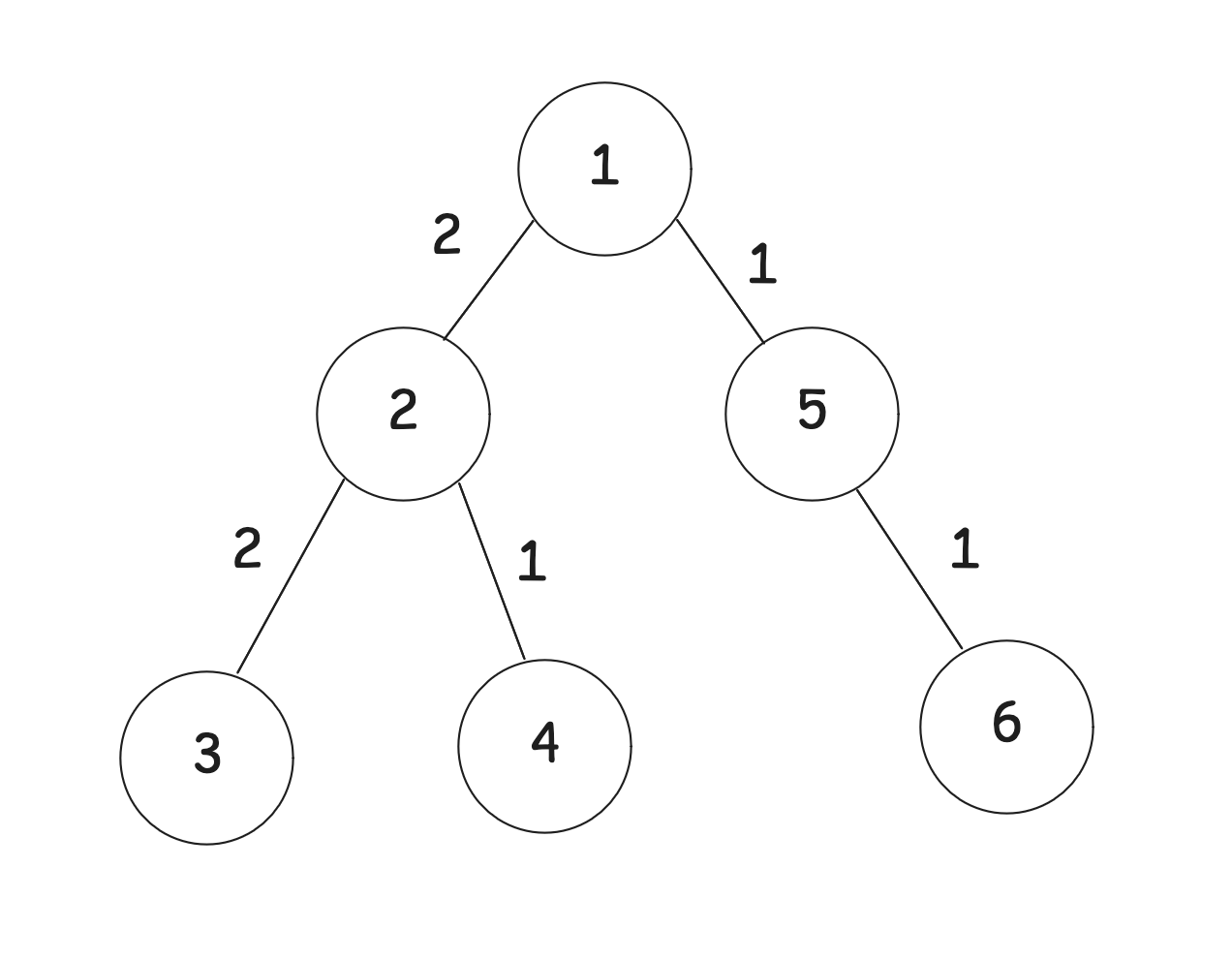

Firstly, all the leaves obviously have 0 possible paths in the subtree. Then, ~5~ has a single ~1~ length path. ~2~ has two direct children, so there are ~2~ paths of length ~1~. The pairs in the subtree of ~1~ are enumerated as such, where we list the intersections and their palindromic path values:

• ~(1,2)\to[2]~
• ~(1,2,3)\to[2,2]~
• ~(1,5)\to[1]~
• ~(1,5,6)\to[1,1]~
• ~(2,3)\to[2]~
• ~(2,4)\to[1]~
• ~(2,1,5,6)\to[1,2,1]~
• ~(3,2,1,5)\to[1,2,1]~
• ~(3,2,1,5,6)\to[1,2,2,1]~
• ~(4,2,1,5)\to[1,2,1]~
• ~(5,6)\to[1]~

Input 2

10
1 2 2
2 3 3
2 4 4
1 5 2
5 6 1
5 7 3
3 8 1
4 9 2
7 10 2

Output 2

20 4 1 1 3 0 1 0 0 0