Ravi recently landed an exciting role at OpenAI and is looking for a new house. Luckily, he has found a street with all the amenities he needs, such as supermarkets, restaurants, and more! Now, he needs to pick the perfect place to live.

The street has houses numbered from ~1~ to ~10^9~, and Ravi can live at any integer house number along the street. Each utility that matters to him is also located at an integer house number. Ravi and one or more utilities can potentially share the same house number (they will live on different floors).

If Ravi chooses to live at house number ~h~, and a utility is located at house number ~p_i~, he incurs an inconvenience equal to ~|h - p_i|~, the distance between them. For example, if a utility is at house number ~2~:

• If Ravi lives at house ~5~, he gets inconvenience ~|5-2| = 3~
• If Ravi lives at house ~1~, he gets inconvenience ~|1-2| = 1~
• If Ravi lives at house ~2~, he gets inconvenience ~|2-2| = 0~

Ravi wants to choose a house that minimises his total inconvenience across all utilities. Can you help him?

Input

The first line contains an integer ~n~ ~(1 \leq n \leq 10^5)~, the number of utilities on Ravi's street.

The second line contains ~n~ integers ~p_1, \dots, p_n~ ~(1 \leq p_i \leq 10^9)~, where ~p_i~ is the house number of the ~i~th utility on Ravi's street. These numbers can be repeated.

Output

Output the house number Ravi should live at to minimise his total inconvenience across all utilities. If multiple ideal locations exist, output the one with the smallest house number.

Example

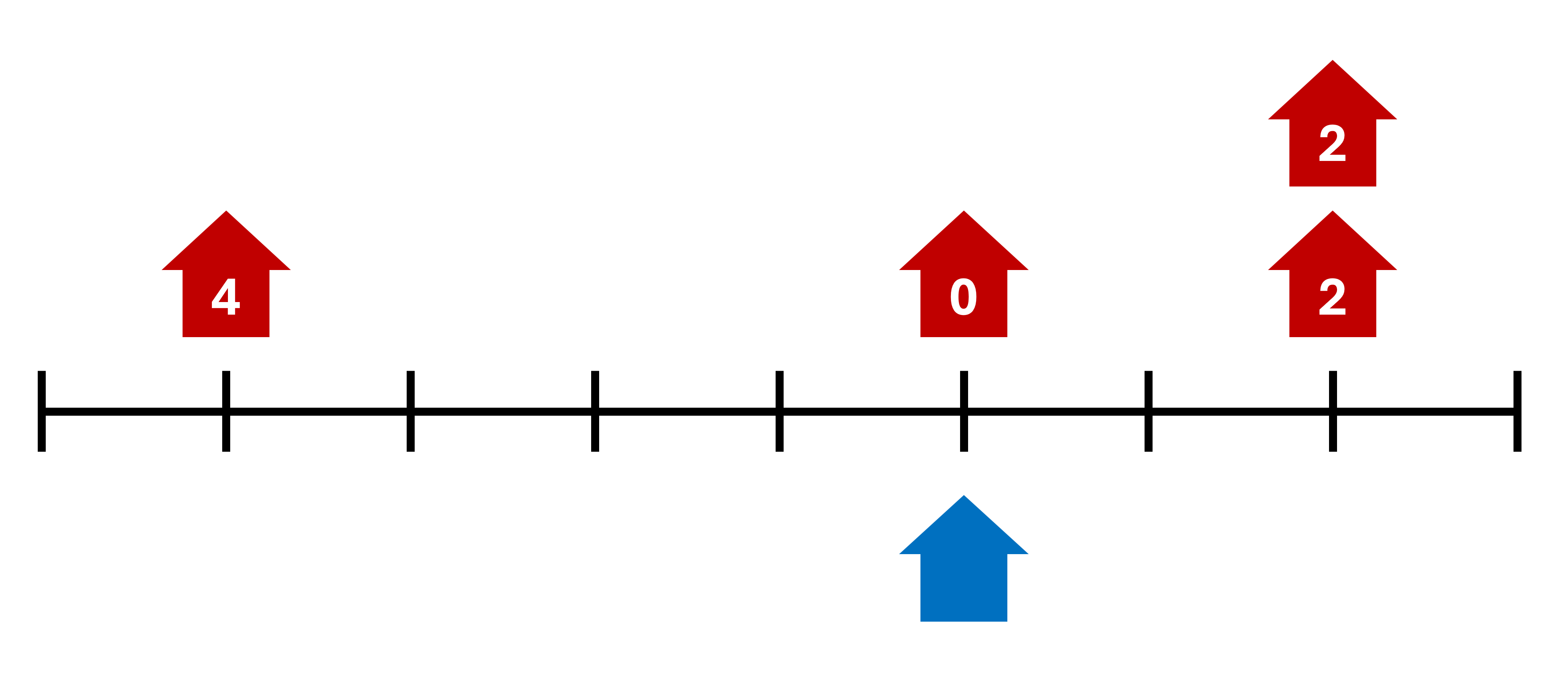
Input 1

4
2 6 8 8

Output 1

6

If Ravi lives at house #6, his total inconvenience is as follows:

• ~|2-6| = 4~ for the first utility.
• ~|6-6| = 0~ for the second utility.
• ~|8-6| = 2~ for the third utility.
• ~|8-6| = 2~ for the fourth utility.

This is a total inconvenience of ~8~, which is the lowest out of any houses he could have chosen.

Input 2

3
4 7 5

Output 2

5

Input 3

2 
1 1000000000

Output 3

1