As RSP's biggest gambling addict, Rory is playing a game of chance. His score starts at zero, and he has a fair ~n~-sided die with faces numbered from ~1~ to ~n~. He repeatedly rolls the die:

• If the number is between ~1~ and ~n-1~, he adds that number to his score.
• If the number is ~n~, he immediately loses.

Rory wins the game if his score reaches at least ~x~. What is the probability that he wins the game?

Input

The first line of the input contains two integers ~n~ and ~x~ ~(2 \leq n, x \leq 1000)~, the number of sides on the die, and the score that Rory needs to win.

Output

Output the probability that Rory wins the game, between 0.0 and 1.0, correct to exactly 6 decimal places.

Example

Input 1

3 2

Output 1

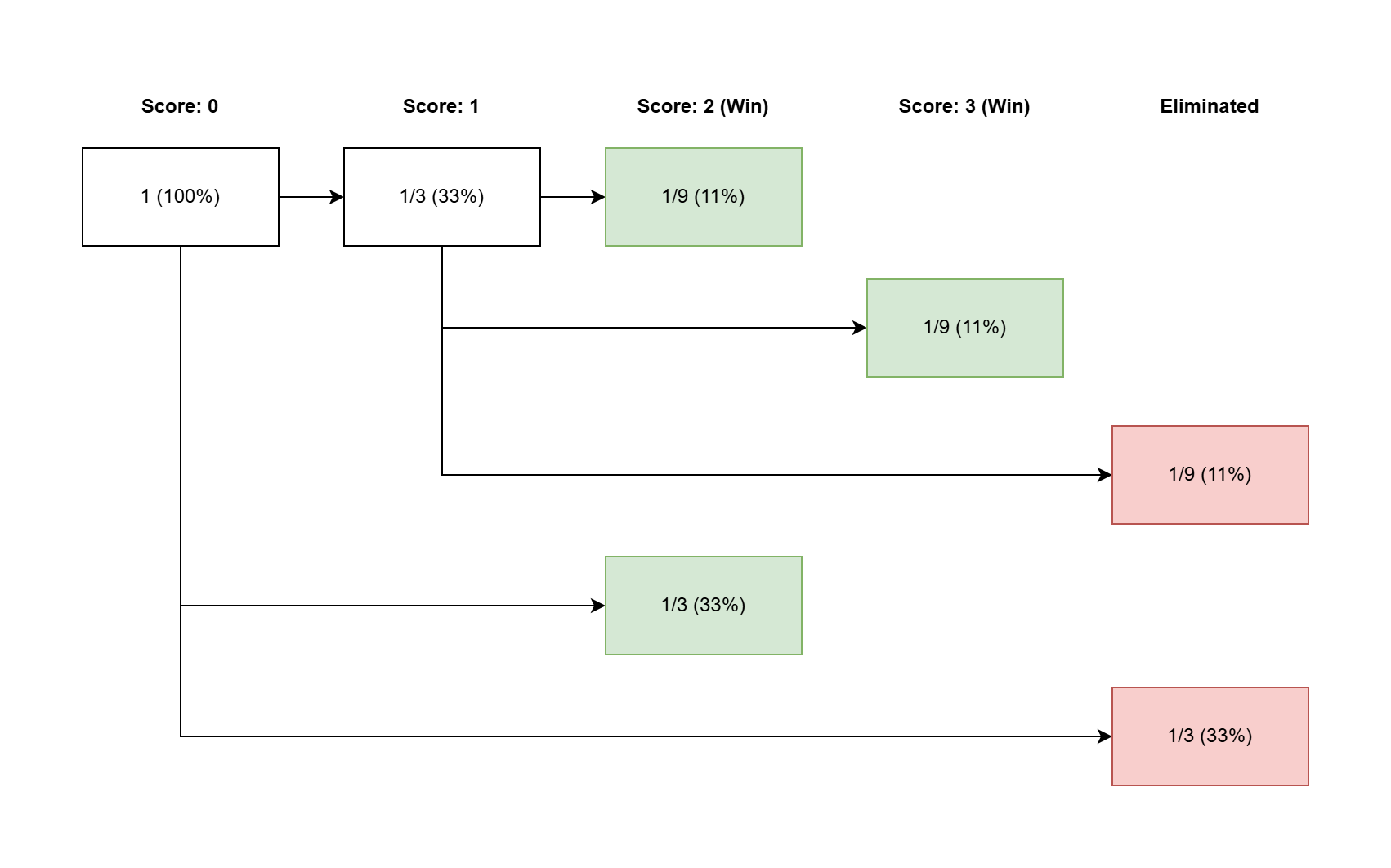
0.555556

Rory has a ~3~-sided die, and he needs to get a score of at least ~2~ to win.

On the first roll:

• He has a ~1/3~ of getting ~1~ point (by rolling a ~1~).
• He has a ~1/3~ chance of winning instantly (by rolling a ~2~).
• He has a ~1/3~ chance of losing instantly (by rolling a ~3~).

If there is a second roll, he is guaranteed to have exactly ~1~ point, so:

• He has a ~2/3~ chance of winning instantly (by rolling a ~1~ or ~2~).
• He has a ~1/3~ chance of losing instantly (by rolling a ~3~).

Overall, he has a ~5/9~ chance of winning, and a ~4/9~ chance of losing.

Input 2

2 4

Output 2

0.062500

Input 3

67 420

Output 3

0.820550