The Adelaide CBD is laid out in what is called a grid plan, meaning streets run at right angles to each other. Conveniently, this means the streets can be represented by a 2D array.

You've decided that you'd like to explore your city a bit more by taking walks around the city. You'll start at the top left of the grid, and would like to eventually reach the top right of the grid.

To reach the top right, you'd like to take a path that follows a specific set of rules. The rules that you'll follow are as follows:

• Your walk will be divided into 2 segments.
• For the first segment of your walk, you will only walk right or down in the grid.
• At any point during the walk, you can move into the second segment. Once in the second segment, you must follow the rules of the second segment for the rest of the walk.
• For the second segment of your walk, you will only walk right or up.

How many different unique paths can you take that follow these rules and finish the walk using a maximum of ~k~ steps?

Input

The first line consists of three integers, ~h~ ~(1 \leq h\leq 100)~, ~w~ ~(2 \leq w\leq 100)~ and ~k~ ~(1 \leq k \leq 1000)~. These represent the height of the grid, the width of the grid, and the maximum number of steps you may take, respectively.

Output

Print the number of unique possible paths that follow the given rules. It is guaranteed that the answer will fit inside a 32-bit integer.

Example

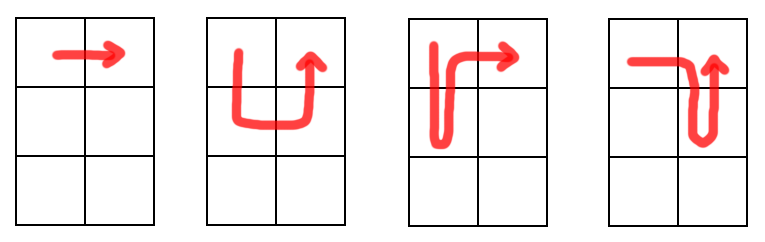
Input

3 2 4

Output

4

Below shows all paths that follow the rule. There is ~1~ path which takes ~1~ step, and ~3~ paths that take ~3~ steps. There are more than ~4~ unique paths, but all other paths take more than ~4~ steps.