The Adelaide Fringe is the largest arts festival in the Southern Hemisphere — a whirlwind of creativity that draws in performers, tourists, and families alike. But with so much going on, it's infamously tricky to market effectively. Many have tried. Most have failed. Now, as the Fringe's newest marketing hire, it's your time to shine, and all eyes are on you.

Adelaide can be modeled as a tree of ~n~ parks, numbered from ~1~ to ~n~, connected by ~n-1~ roads. Victoria Square, the beating heart of the city, is park ~1~. Each park already has a Fringe poster, marked with some initial "swag value", but you know they could be so much cooler.

You begin your journey at park ~1~. Each day, your supervisor tells you to walk from your current park to some target park ~X~, admiring every poster you pass. Then, using the inspiration from your walk, you must design a brand new poster. This poster will have a swag value equal to the maximum swag value you saw along the path, plus one (thanks to your creative genius). You'll then use this new poster to replace every poster along the walk from park ~X~ to park ~Y~. Finally, you must report the swag value of your new poster design. The next day, your starting point is park ~Y~.

Can you carry Adelaide's advertising to unimaginable levels of swag?

Input

The first line contains an integer ~n~ (~1 \leq n \leq 10^4~), the number of parks.

The next line contains ~n~ integers ~S_1 \dots S_n~ (~1 \leq S_i \leq 10^9~), representing that the ~i~th park initially has a poster with a swag value of ~S_i~.

The following ~n - 1~ lines each contain two integers ~A~ and ~B~ (~1 \leq A, B \leq n~), indicating a bidirectional path between parks ~A~ and ~B~. It is guaranteed that the graph forms a tree.

The next line contains an integer ~d~ (~1 \leq d \leq 10^5~), the number of days you are working.

The next ~d~ lines each contain two integers ~B~ and ~C~ (~2 \leq B, C \leq n~), indicating that on this day, you must admire all posters on the walk from your current park to park ~B~, then update the posters along the walk from park ~B~ to park ~C~.

Output

Print ~d~ lines. Each line should contain a single integer, the new swag value assigned to all posters along the path from park ~B~ to park ~C~ on that day.

Example

Input 1

10
2 5 4 3 1 7 2 4 10 3
1 2
1 7
2 3
2 4
2 5
4 6
7 8
7 9
8 10
3
8 9
5 1
6 4

Output 1

5
6
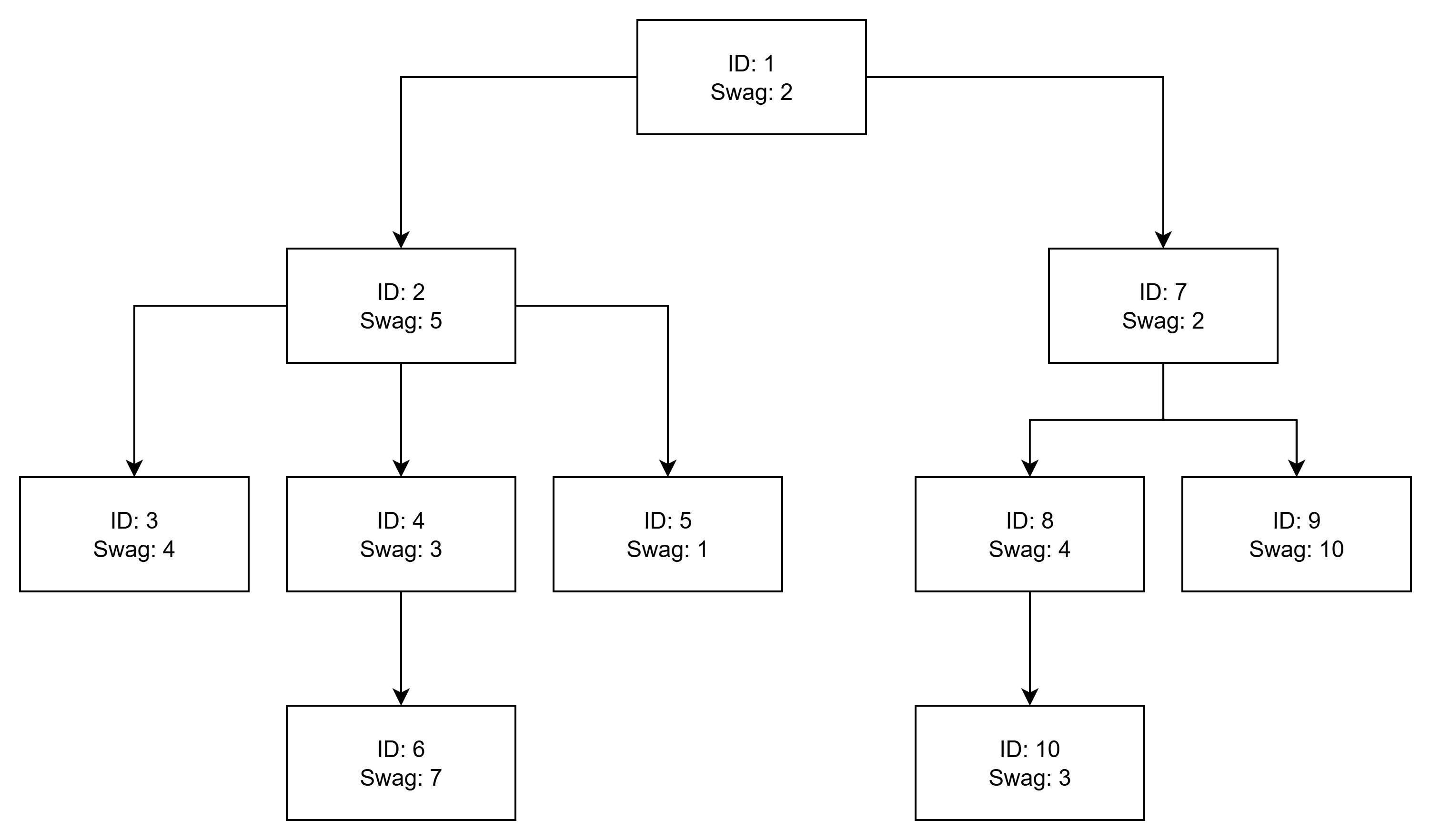
8

This is the initial state of the parks, including their posters and connections.

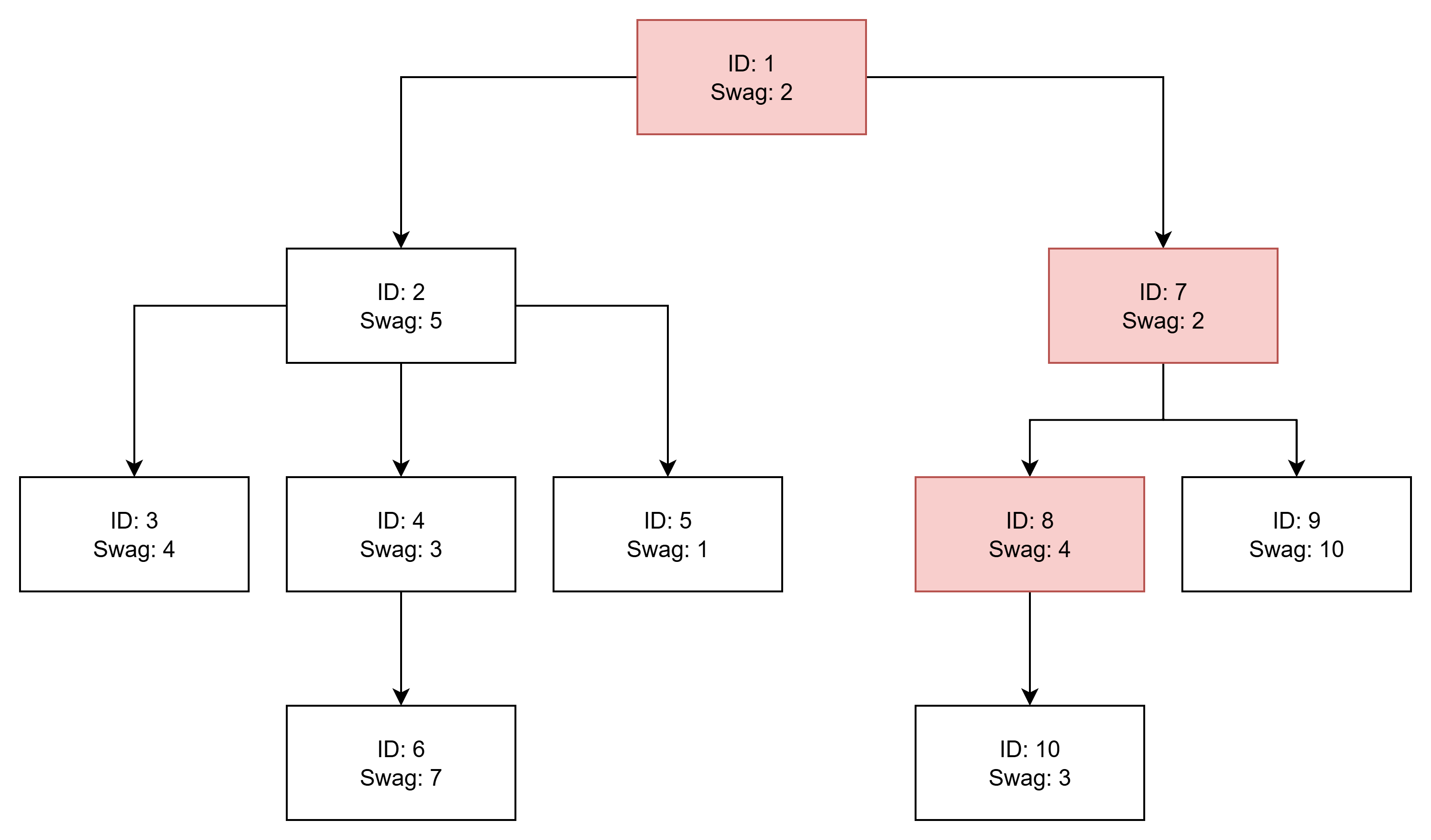
On day 1, walk from park ~1~ to park ~8~. The maximum "swag value" on this path is ~4~.

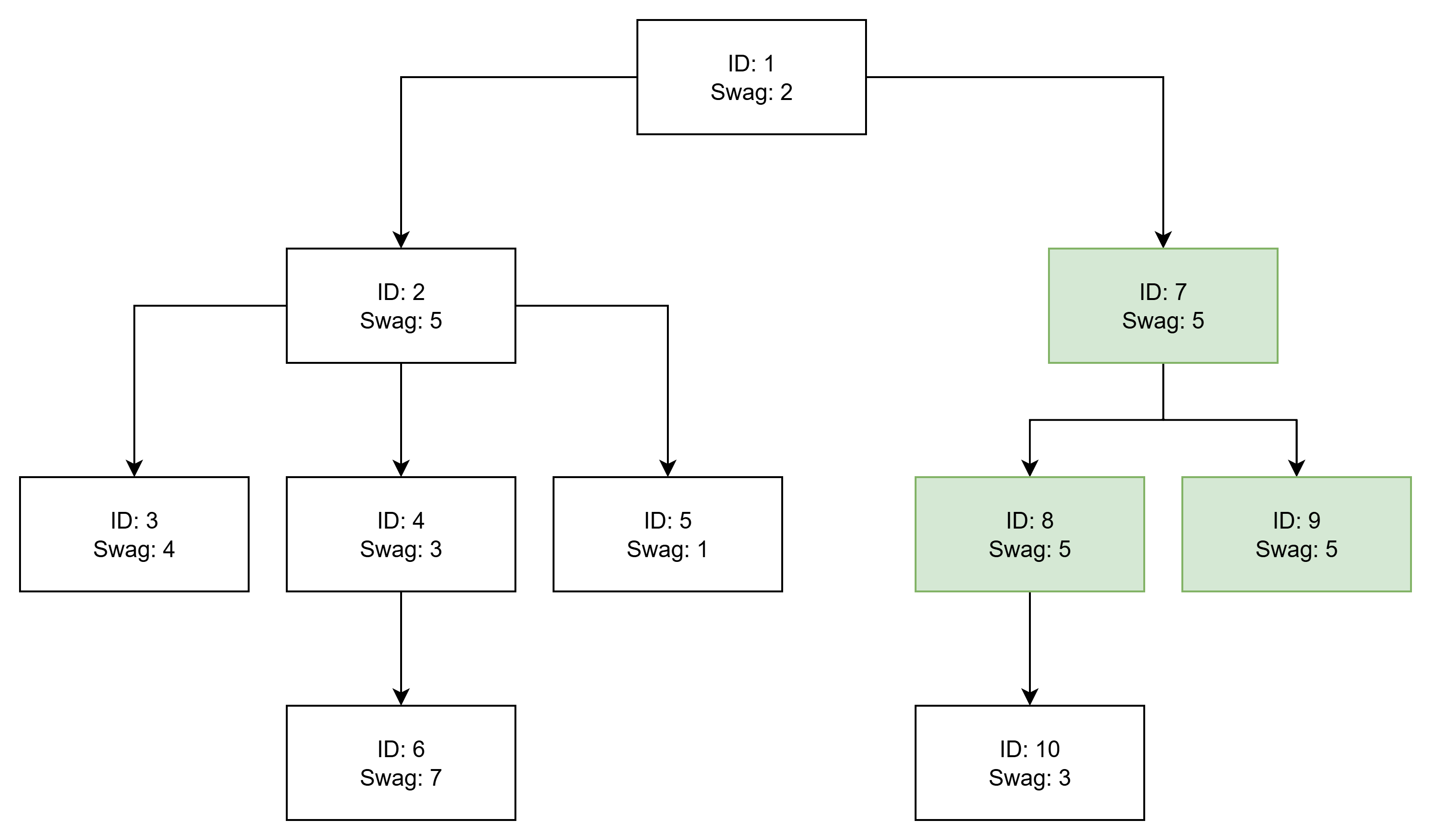
Therefore, when we walk from park ~8~ to park ~9~, we make all posters on this path have a swag value of ~4+1 = 5~.

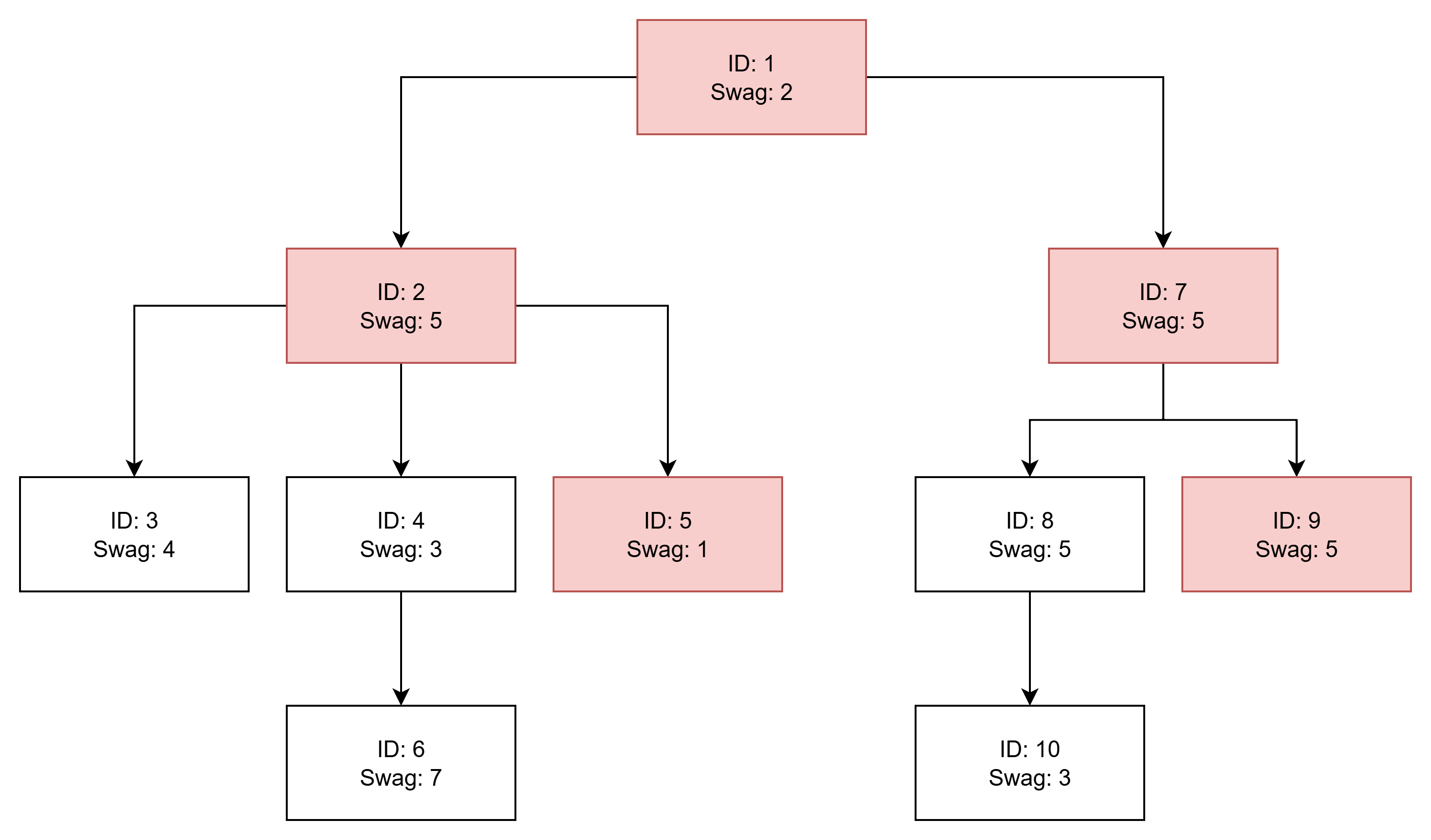
On day 2, walk from park ~9~ to park ~5~. The maximum "swag value" on this path is ~5~.

Therefore, when we walk from park ~5~ to park ~1~, we make all posters on this path have a swag value of ~5+1 = 6~.

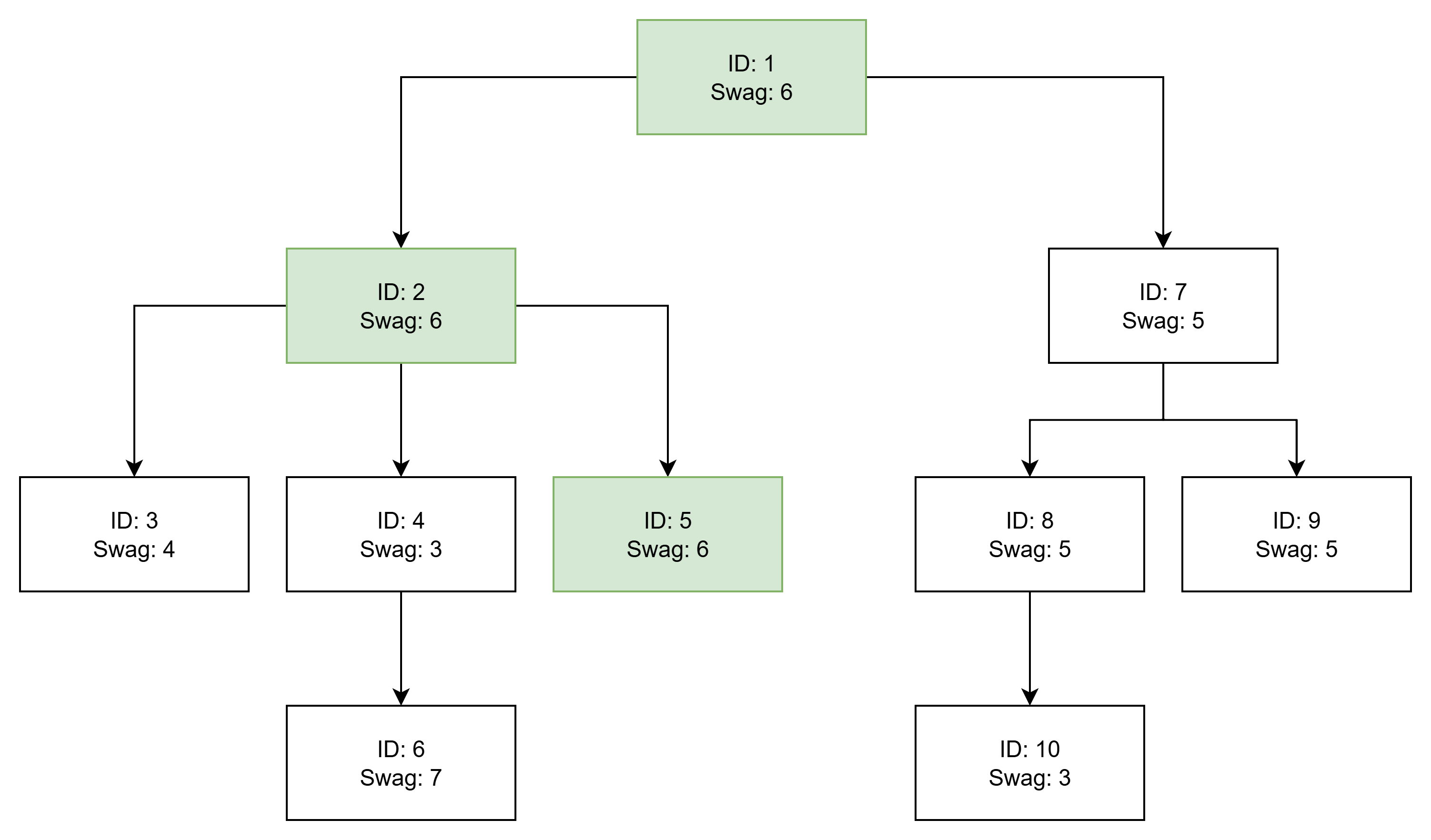
On day 3, walk from park ~1~ to park ~6~. The maximum "swag value" on this path is ~7~.

Therefore, when we walk from park ~6~ to park ~4~, we make all posters on this path have a swag value of ~7+1 = 8~.

Input 2

15
4 3 3 7 2 1 5 1 8 6 3 2 4 1 10
1 2
1 7
2 3
2 4
2 5
4 6
7 8
7 9
8 10
10 11
10 12
12 13
12 14
12 15
7
2 3
1 5
6 10
15 8
3 1
1 9
8 14

Output 2

5
6
8
11
12
13
14

The first location of a day can be the same as the last location of a previous day.