Footy Fanatics
At Adelaide Oval, someone's mixed the Port Power and Adelaide Crows fans together! They hate each other, and would rather be with supporters of their own team. Given a field of footy fans, you can make one of four operations:
- Move a fan
unit up, at the cost of
inconvenience.
- Move a fan
unit down, at the cost of
inconvenience.
- Move a fan
unit left, at the cost of
inconvenience.
- Move a fan
unit right, at the cost of
inconvenience.
With these operations, you want to move the Port and Crows fans, so that they can be segregated by a single, vertical or horizontal fence. What is the minimum total amount of inconvenience required to do this?
Input
The first line consists of an integer
, the number of footy fans on the field.
The next line consists of 4 integers, ,
,
and
, representing the cost of moving any fan, up, down, left and right, respectively.
The next lines contain
,
, and
, where
is the identity of the fan (
Port or Crows) who is standing at
.
Output
Output the minimum cost required to move the fans, so that Port and Crows players can be separated by a horizontal or vertical line.
Clarifications
- Two fans can occupy the same square at once.
- However, the input won't have two fans in the same square.
- Two fans can move past each other, even if they support opposing teams.
- You are able to move fans outside of the question's bounds (for example, negative coordinates are OK).
- In this problem, moving to the right is +x, moving down is +y.
Example
Input 1
8
4 5 2 1
P 1 1
P 1 5
P 3 6
P 4 3
C 2 2
C 3 4
C 5 2
C 6 5Output 1
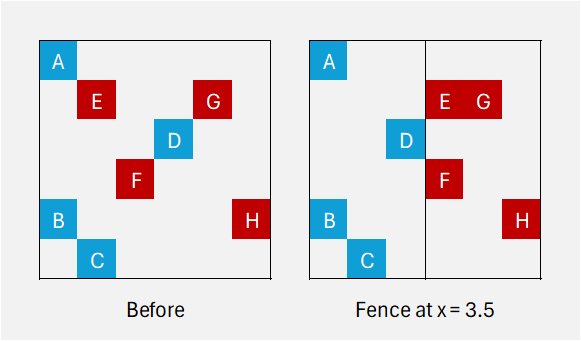
5The optimal cost to separate the Port and Crows fans can be achieved by:
- Moving fan E right
squares.
cost.
- Moving fan F right
square.
cost.
- Moving fan D left
square.
cost.
Overall, it takes a minimum of cost to separate the fans.
Input 2
2
2 7 6 3
P 1 1
C 2 2Output 2
0The fans are already separated.
Input 3
6
2 3 2 5
P 1 1
P 4 3
P 5 5
C 2 4
C 4 5
C 5 2Output 3
9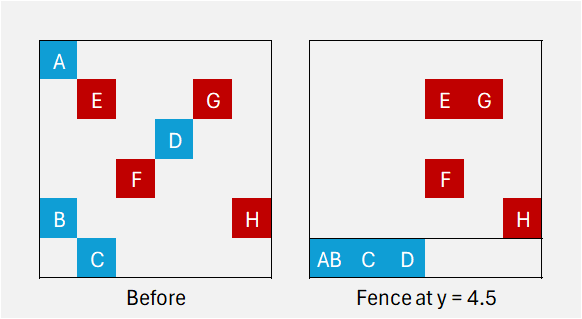
Comments