You might have wondered where Adelaide's trains go when they're not in use. Why, to the end of the line, of course!

Each train is numbered from ~1~ to ~n~, and when service ends for the day, all the trains arrive at the end of the line in some arbitrary order. There, the track splits into a side branch and a tunnel.

The line manager dreams of sending the trains into the tunnel in perfect ascending order, from ~1~ to ~n~. However, the side branch is the only space where trains can manoeuvre around each other, and that dream is often too much to ask.

There are two key rules:

• Once a train enters the side branch, it can later enter the tunnel, but cannot return to the arrival line.
• Once a train enters the tunnel, it cannot come back out.

Instead of perfection, the manager now settles for a more modest goal, to send as many trains into the tunnel from the sequence ~1~ to ~n~ as possible. Any train that doesn't fit into that sequence must stay out in the cold.

Given the order in which the trains arrive, and assuming perfect coordination, what is the maximum number of trains that can be sent into the tunnel in ascending order?

Input

The first line contains an integer ~n~ (~1 \leq n \leq 10^5~), the number of trains that are being put away.

The next line contains ~n~ integers from ~1~ to ~n~, representing numbers of trains that are being put away, in order. The leftmost train is the one at the front of the queue.

Output

Output the maximum number of trains that can enter the tunnel, if they are only allowed to be put in ascending order.

Clarifications

In each test case, all trains have a unique number and all trains from ~1~ to ~n~ are present.

Example

Input 1

5
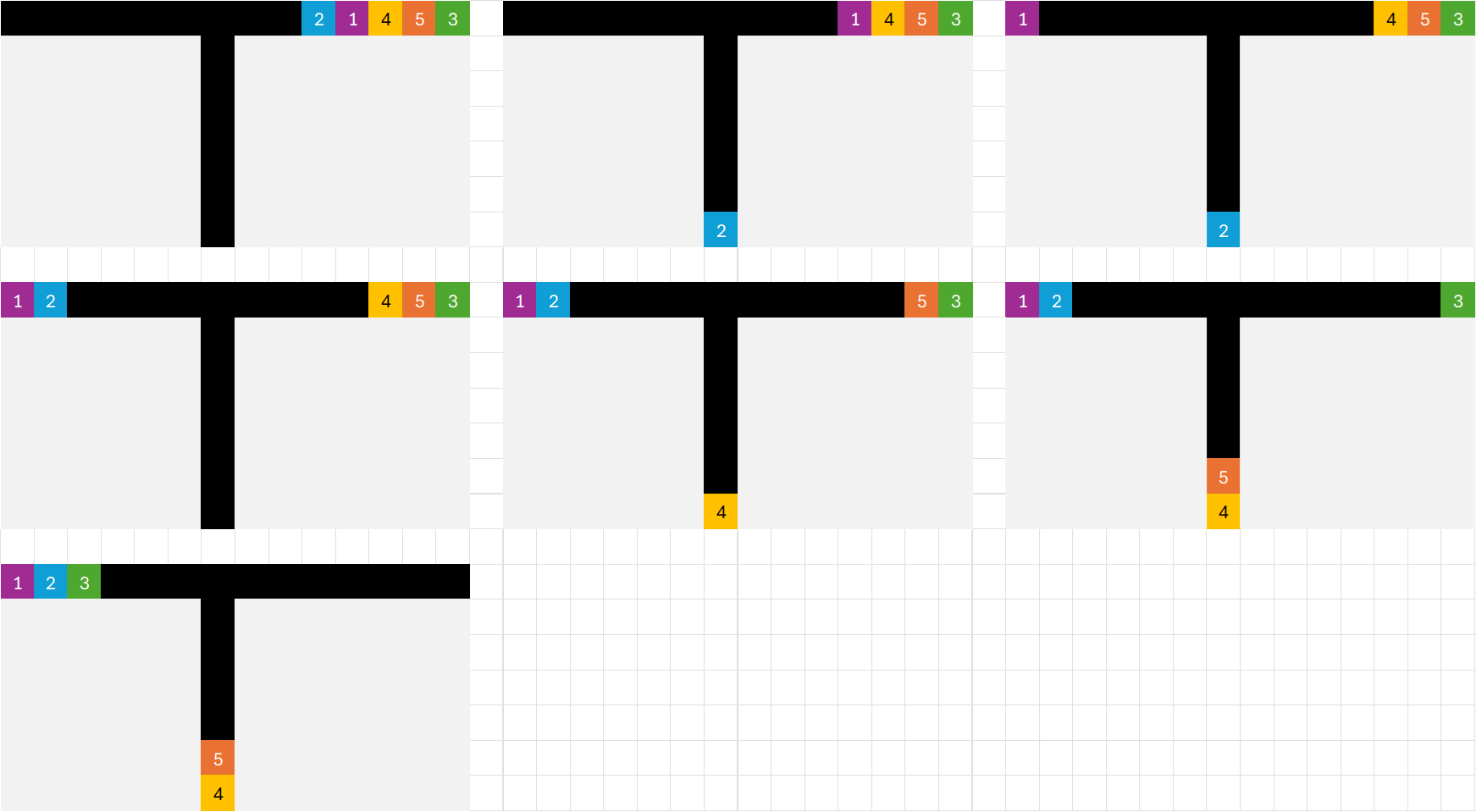
2 1 4 5 3

Output 1

3

3 trains can be placed in ascending order via the following operations.

• Put ~2~ in the side branch.
• Put ~1~ in the tunnel.
• Put ~2~ in the tunnel.
• Put ~4~ on the side branch.
• Put ~5~ on the side branch.
• Put ~3~ in the tunnel.

It can be shown that this is the maximum number of trains that can be placed in ascending order.

Input 2

9
1 2 8 5 4 3 9 6 7

Output 2

7

Input 3

7
7 6 5 4 3 2 1

Output 3

7