Dreaming of Shapes
Your toddler just gave you a drawing, and... well you don't know what it is. "Shapes!" is all they say. "Shapes! Shapes!". But which shapes?
The drawing is made of several points, connected by several, straight lines. A shape is considered a closed loop of unique points, that can be made by tracing over these lines.
For example, the following drawing has unique kinds of shapes:
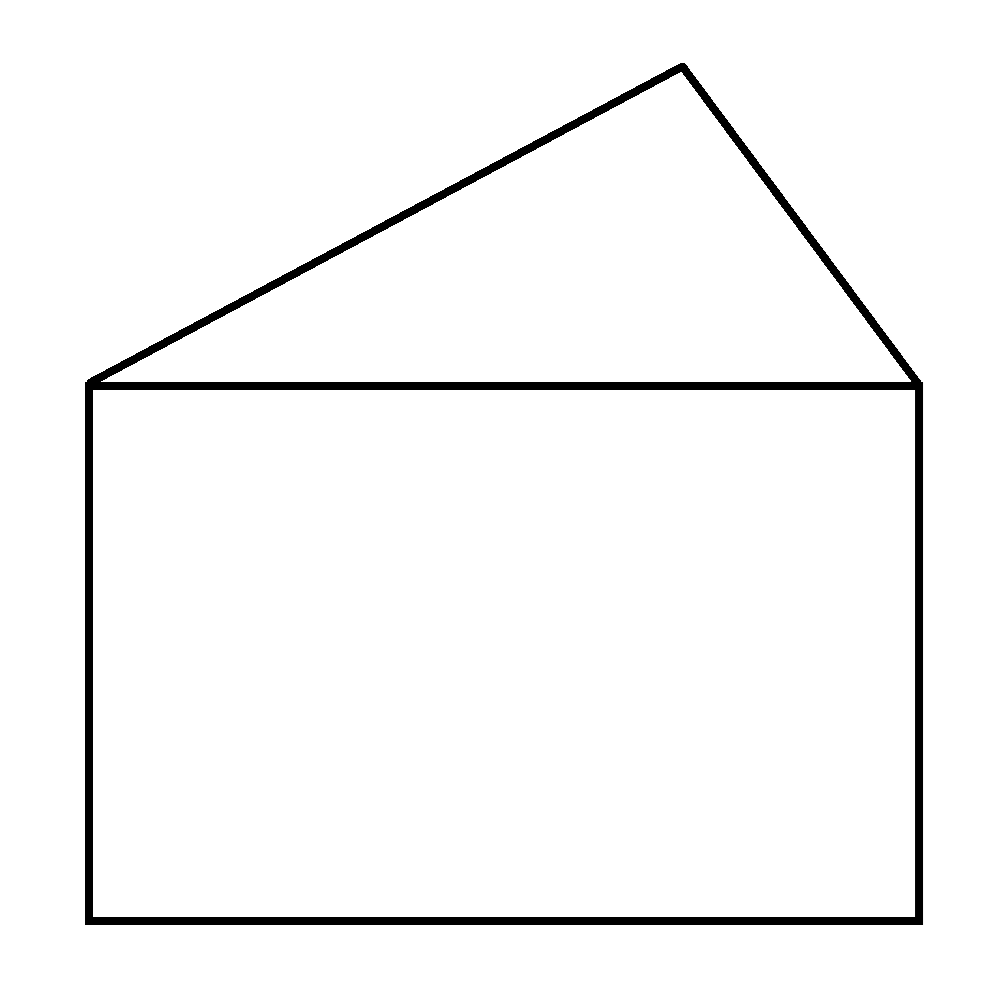
A -sided shape:
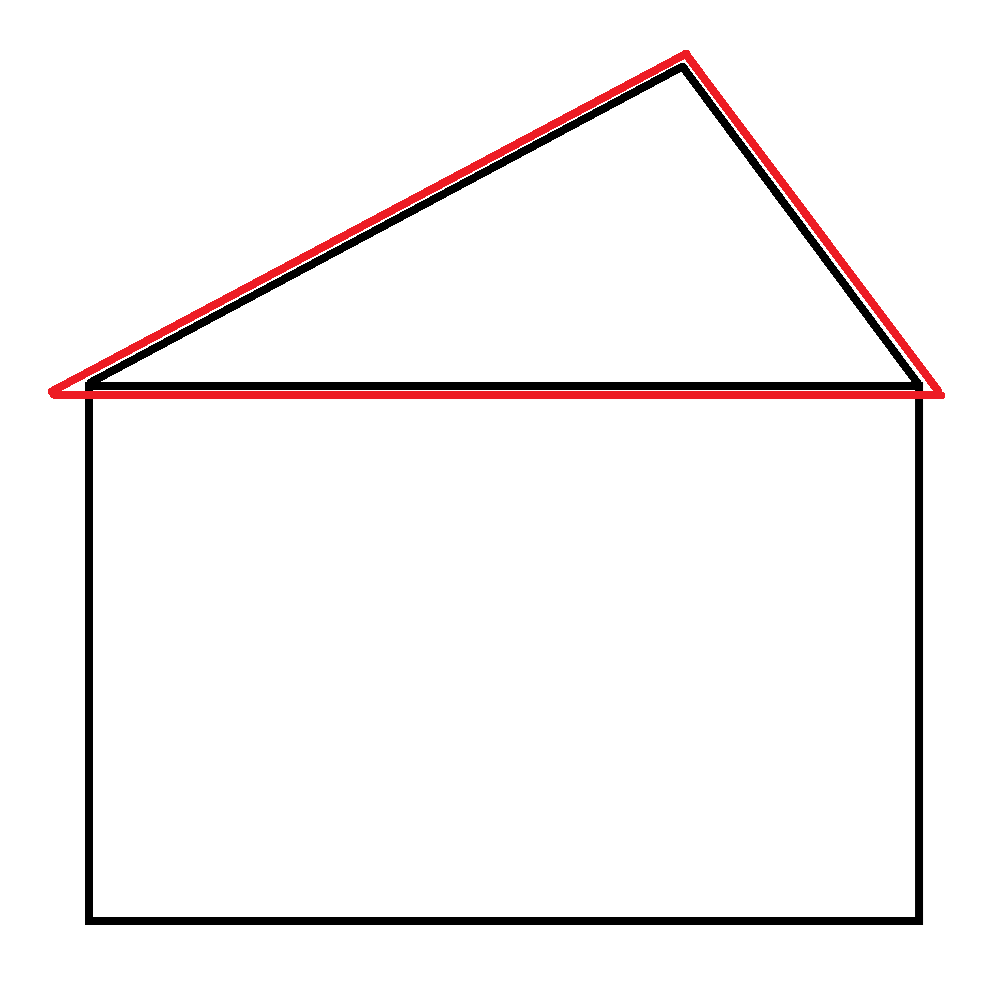
A -sided shape:
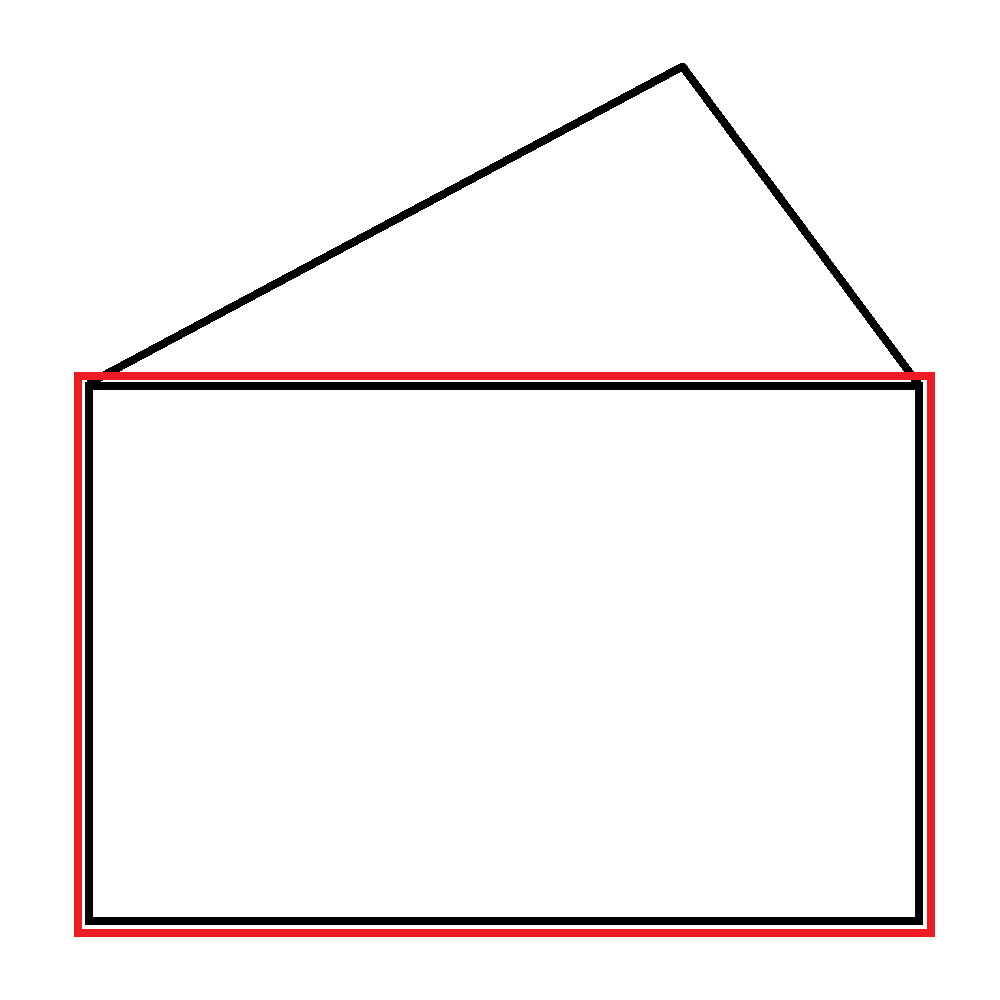
A -sided shape:
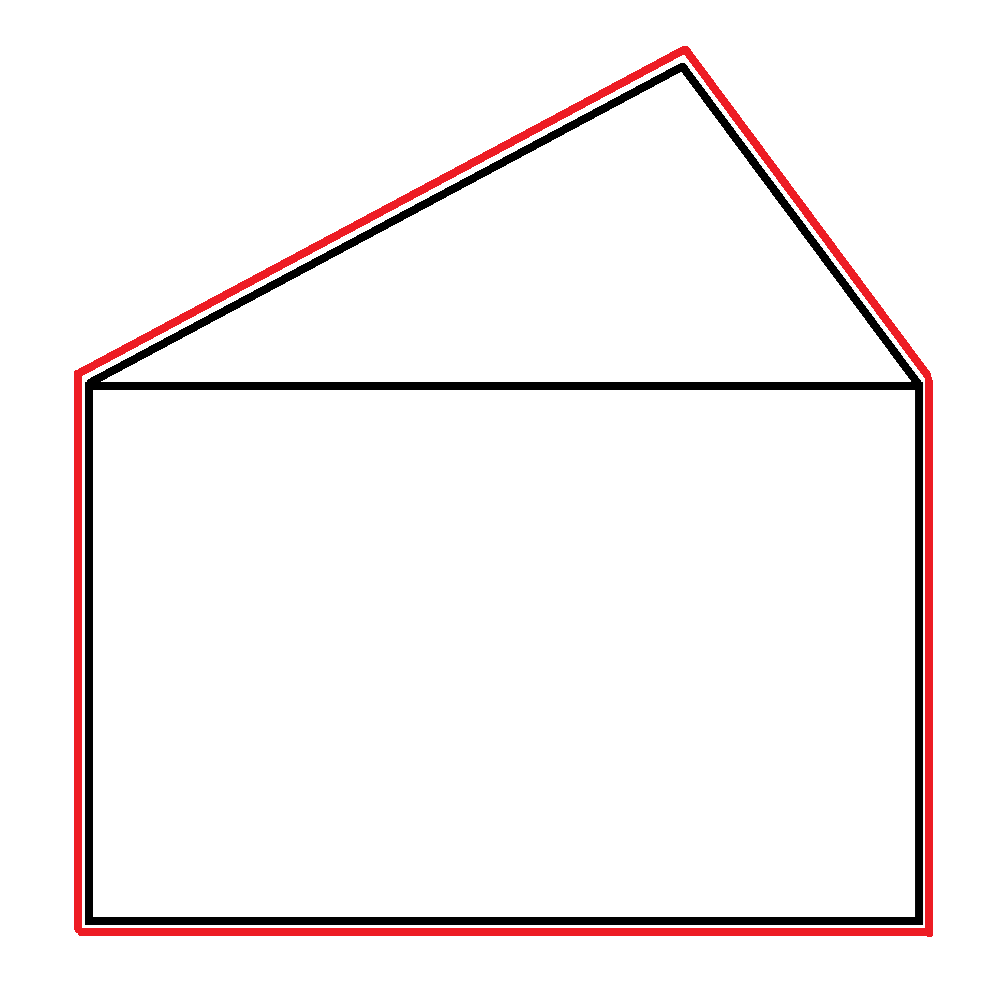
So there would be unique kinds of shapes overall.
The following drawing has unique kinds of shapes:
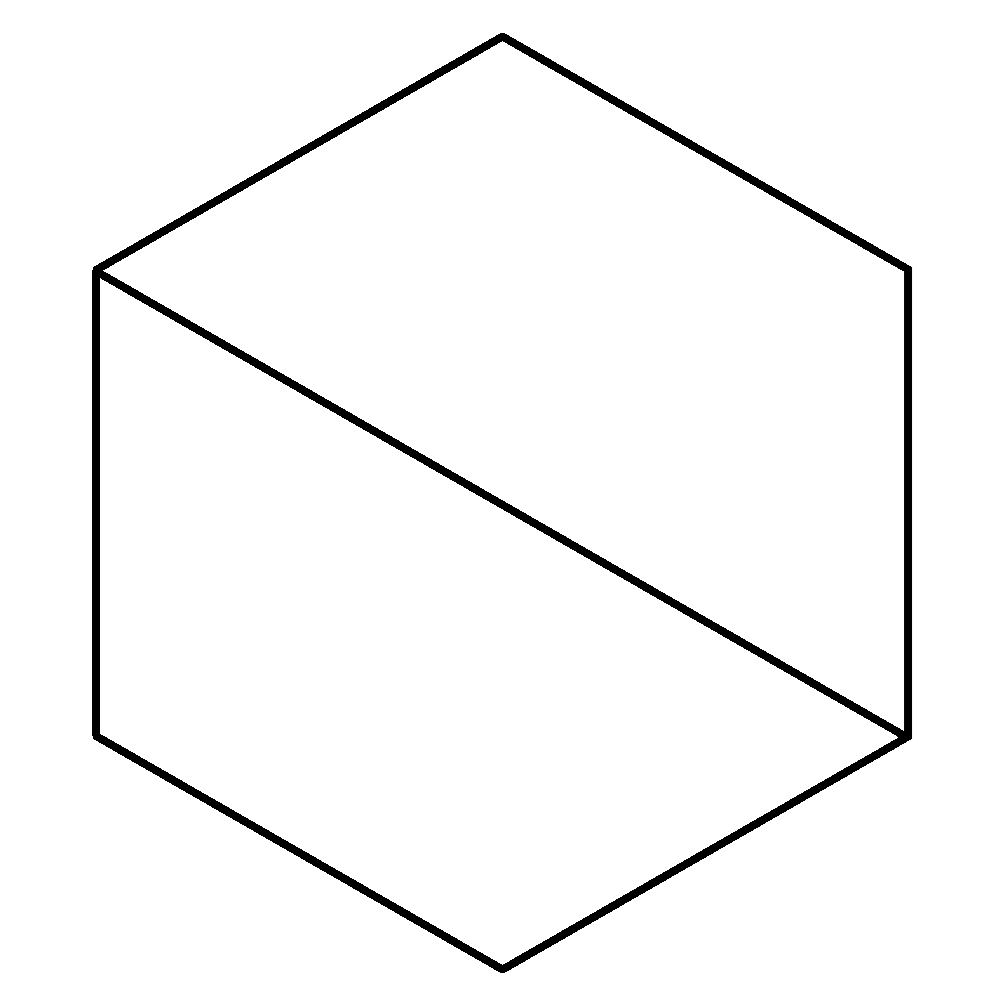
There is a -sided shape and a
-sided shape.
Note: Don't worry too much about how the shapes look. All that matters is how many edges are in the loop!
How many shapes can be made from your child's beautiful artwork?
Input
The first line consists of an integer
, the number of points in the drawing. Each point is numbered from
to
.
The second line consists of an integer
, the number of lines in the drawing.
The next lines are in the form
, indicating that there is a line between points
and
.
Output
Output the number of unique shapes you can make from the drawing, by tracing over a continuous path.
Example
Input
5
6
1 2
1 3
2 4
2 5
3 4
4 5Output
3See the first example above for an explanation, this is the same shape.
Input
6
7
1 2
2 3
3 4
4 5
5 6
6 1
1 4Output
2See the second example above for an explanation, this is the same shape.
Comments