Thankfully, you've dodged every asteroid. Nice flying! But just as you're catching your breath... WEEOO! WEEOO! Alarms blare through the cabin.

You glance to your left. A massive comet is barreling straight toward your ship, and there's no time to react.

CRASH! The impact slams you to the floor. Everything goes black.

When you wake, the cabin is eerily silent. The stars outside are unfamiliar, scattered across a vast and empty stretch of space. The comet must have knocked your ship far off course. You're alone, and hopelessly lost.

At least the stars are beautiful. You wonder how many constellations (groups of connected stars) that result from the ~s~ stars outside, after connecting all stars no more than ~d~ light years apart. In this great void, its up to you to find beauty.

Input

The first line consists of a single integer ~s~ ~(1 \leq s \leq 500)~, the number of visible stars.

The next ~s~ lines consist of two integers ~r~ and ~c~ ~(0 \leq r, c \leq 10^9)~, the row and column coordinates of a star (in light years).

The next line consists of a single integer ~q~ ~(1 \leq q \leq 500)~, the number of queries.

Each of the following ~q~ lines contains a single integer ~d~ ~(0 \leq d \leq 10^9)~, a distance threshold.

Output

For each query, calculate the number of constellations that are formed from the stars you can see, when connecting all stars no greater than ~d~ light years apart.

Clarifications

• Each star is in a unique location.
• Distance between two stars is Euclidean Distance. That is to say, if one star is at ~(r_1, c_1)~ and another is at ~(r_2, c_2)~, then the distance between them is ~\sqrt{(r_1-r_2)^2 + (c_1-c_2)^2}~.

Example

Input 1

7
0 0
0 2
1 10
1 14
3 8
3 14
4 1
3
5
3
7

Output 1

2
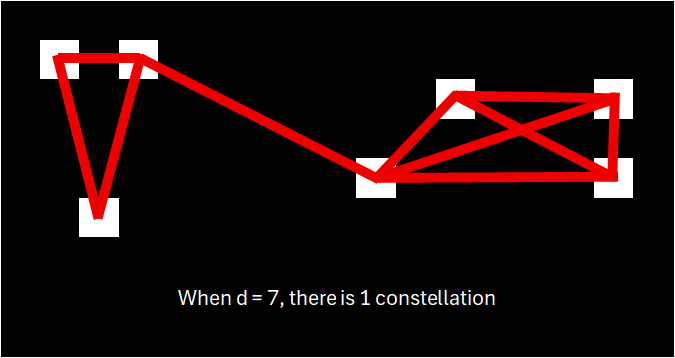
4
1

The number of constellations in each case are shown below.

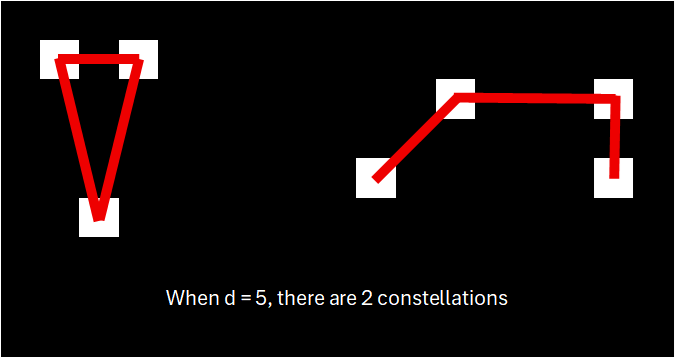
<< In Progress >>

Input 2

5
0 0
0 1
1 0
1 1
2 2
3
0
1
2

Output 2

5
2
1

Input 3

6
0 0
0 1
0 3
0 4
0 6
0 7
3
2
0
1

Output 3

1
6
3