You are a master collector of numbers. Over the years, you've gathered a treasure trove of integers, each one rarer than the last. Now, as you step into retirement, it's time to do what all collectors do: fuse your entire collection into one single number, by multiplying them all together.

But what form should this final number take? After much thought, you decide it must be a perfect square, a number polished and flawless.

Of course, your collection might not multiply to be square right away. Luckily, you have a secret talent. For any number in your trove, you can "carve" it down into any one of its factors. With careful carving, you can reshape your hoard so they multiply to make various different squares.

How many distinct perfect squares can you create by carving your numbers, then multiplying them?

Input

The first line consists of an integer ~n~ ~(1 \leq n \leq 10^5)~, the amount of numbers in your treasure trove.

The next line consists of ~n~ integers ~A_0, \dots,A_n~ ~(1 \leq A_i \leq 10^5)~, the value of the numbers in your treasure trove.

Output

Output the number of distinct squares you can create by replacing any set of numbers in your trove by any of its factors, then multiplying them all together. Since the answer may be very large, please return it modulo ~10^9 + 282757~.

Clarifications

• A perfect square is a number whose square root is an integer. For example, ~4~ is a perfect square, because ~\sqrt4 = 2~.
• Please submit this problem using PyPy, if you're using Python.

Example

Input 1

6
2 6 3 4 1 7

Output 1

6

There are 6 distinct squares you can create by carving down this set of numbers and multiplying them, as shown below. The blue numbers represent those that have not been carved, whereas the red numbers represent those that have. Note that for some squares, the configuration shown is not the only way to produce that number.

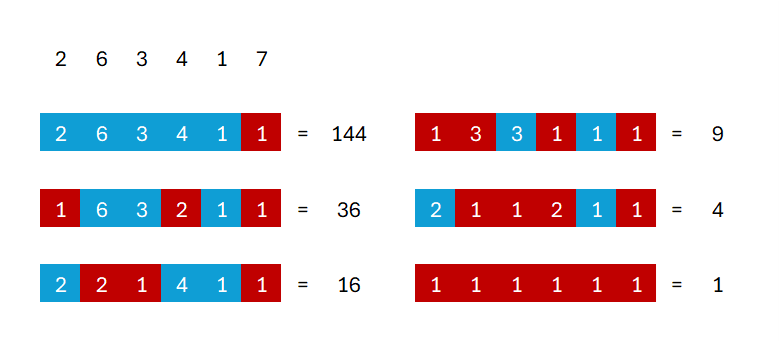
Input 2

4
2 4 6 2

Output 2

3

Input 3

5
13 5 2 3 7

Output 3

1