After a long day of free-ranging, Farmer Shayla wants to bring their chickens back to the coop. However, their chickens have very short attention spans and need to be coaxed with shiny, jingly bells to follow them around.

At Shayla's farm, there are ~n~ fields numbered from ~1~ to ~n~, and connected by bidirectional roads. The chickens start at field ~1~, and Shayla wants them to follow along with them to field ~n~, where the coop is. However, the chickens will refuse to traverse any road more than ~x~ meters long, unless Shayla has tied at least ~x~ bells to their belt.

Shayla has an unlimited number of bells, but tying bells to their belt can be a time-consuming process. What is the minimum number of bells required for Shayla to be able to get their chickens home safely?

Input

The first line contains two integers ~n~ ~(1 \leq n \leq 10^5)~ and ~m~ ~(1 \leq m \leq 10^5)~, the number of fields and the number of roads on Shayla's farm.

The next ~m~ lines contain 3 integers ~a~ ~(1 \leq a \leq n)~, ~b~ ~(1 \leq b \leq n, a \neq b)~ and ~x~ ~(1 \leq x \leq 10^9)~, indicating that there is a bidirectional road connecting fields ~a~ and ~b~ that is ~x~ meters long.

Output

Output the minimum number of bells that Shayla needs to tie to their belt, so that his chickens will follow them from field ~1~ to field ~n~.

Clarifications

• Two fields can be connected by multiple roads.
• There is guaranteed to be at least one path from field ~1~ to field ~n~.

Example

Input 1

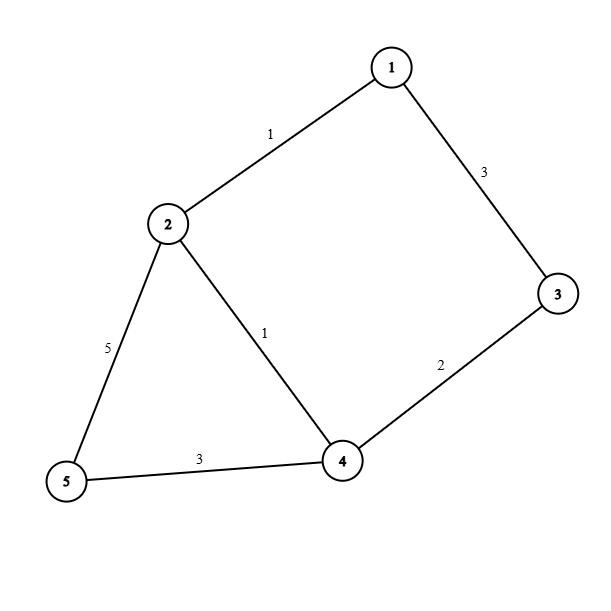
5 6
1 2 1
1 3 3
3 4 2
2 5 5
4 2 1
4 5 3

Output 1

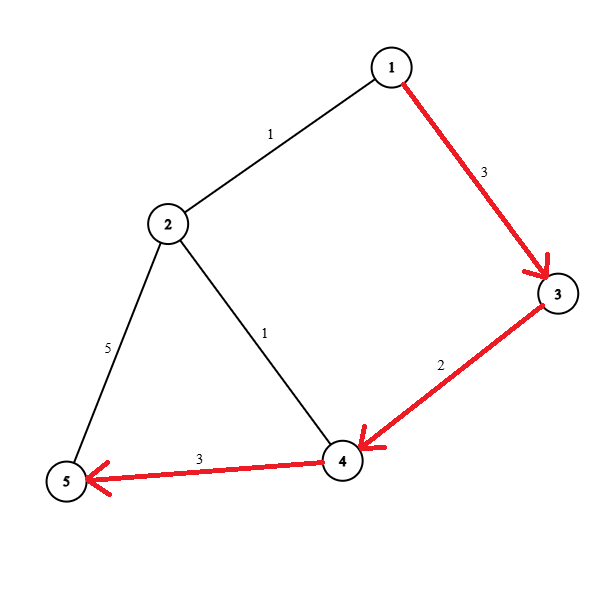
3

If Shayla ties ~3~ bells to their belt, his chickens will follow them along all roads no more than ~3~ meters long. In this case, we can take the chickens from field ~1~ to field ~5~ by going from ~1 \rightarrow 3 \rightarrow 4 \rightarrow 5~. No road along this path is longer than ~3~ meters, so their chickens will follow them the whole way.

It can be shown that ~3~ is the minimum number of bells required to get the chickens home. Note that this isn't the only path with a longest road of ~3~ meters from ~1~ to ~5~.

Input 2

6 8
1 6 10
1 2 1
2 3 2
3 4 3
3 6 8
4 5 4
4 6 2
5 6 5

Output 2

3

Input 3

2 5
1 2 3
1 2 8
1 2 1
1 2 6
1 2 7

Output 3

1