It's true! Cats can squish into basically any-sized container that you put them in, and it's great fun to see this in practice.

By a stroke of luck, you've found an infinite number of cats and ~n~ bricks of unit length, unit width and varying height. You've placed the bricks side-by-side to make a fort, and want to put as many cats in it as possible. A cat has a volume of ~v~ units, and can squish to any shape. However, the cats are shy, and want to be placed no higher than the tallest brick in the fort.

How many cats can occupy your brick palace?

Input

The first line contains two integers ~n~ and ~v~ ~(1 \leq n \leq 10^5, 1 \leq v \leq 10^9)~, the number of bricks in the fort, and the volume of one cat.

The next line contains ~n~ integers ~h_1, \dots, h_n~ ~(1 \leq h_i \leq 10^5)~, where ~h_i~ represents the height of the ~i~th brick in the fort. To the left of the first brick and the right of the last one, you can imagine there is some infinitely-tall wall.

The cats don't need to be in blocky, "unit" spaces.

Output

Output the number of cats you can fit in the fort, such that no part of any cat is positioned higher than the tallest brick.

Example

Input 1

11 5
1 3 4 2 6 1 6 5 3 3 4

Output 1

4

At most ~4~ cats can be placed in this structure without exceeding a height of ~6~ (the tallest brick), as shown below.

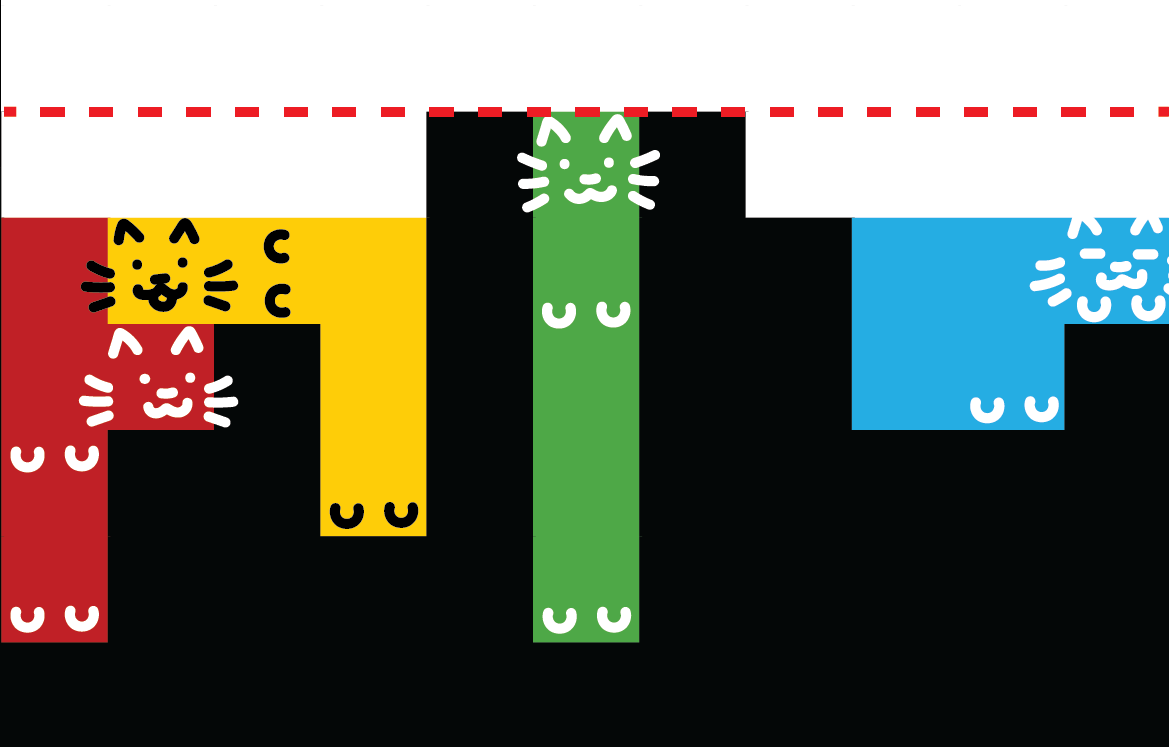
Input 2

11 4
6 5 4 3 2 1 2 3 4 5 6

Output 2

6

Input 3

11 4
6 5 4 3 2 6 2 3 4 5 6

Output 3

4

Input 4

5 1
10 10 10 10 10

Output 4

0