Animal Farm
While Tom wasn't looking, the various farm animals in his field formed a caste system, separating into two classes who absolutely hate each other and blame each other for all of their misfortunes. Unfortunately, Tom needs to move them into a new pen and he has already laid out the convex fenced perimeter of the new pen. Before he undoes all of his hard work, he wants to verify if the pen is suitable or not first.
The two classes of animals cannot be mixed together since they despite each other, though the one thing that does unite them is socialism. Thus, for the animals to live in harmony, the pen must be divided into two sections of equal area by one additional line of fence connecting two of the perimeter fence posts. If it is impossible to divide the existing pen as such, then Tom must seek another solution before the working class of animals unite to overthrow the farm management...
Input
The first line contains a single integer
, the number of fence posts which form the vertices of the pen. The posts are labelled
through
.
The next lines each contain two space-separated integers
and
, the coordinates of the
th fence post. The
th fence post is also connected via fence to the
th post, except for the final
th post which is connected to the
st post, such that the fence forms a loop enclosing a simple polygon. This means that all the fences are straight lines, and they will never cross over or intersect each other. Moreover, the polygon is guaranteed to be convex. This means that any line drawn between two points in the polygon cannot go outside of the polygon, so there are no 'dents'.
Output
If the fenced pen can be divided into two sections of equal area using a straight line between two of the existing fence posts, output 'Yes', otherwise output 'No'.
Example
Input 1
4
0 0
0 1
1 1
1 0Output 1
YesThis shape is a simple square. Dividing across either of the diagonals would lead to equally-sized areas.
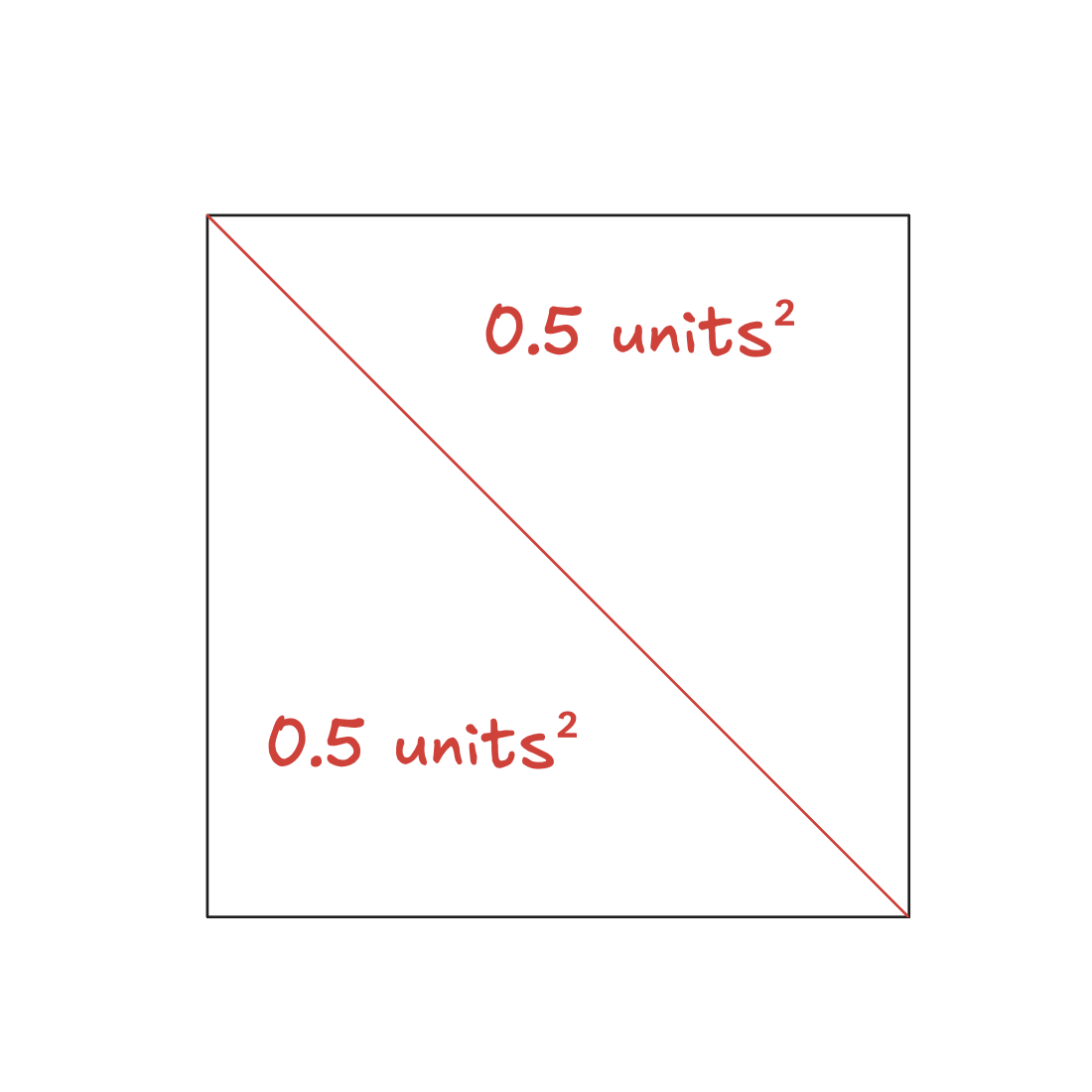
Input 2
5
0 0
0 1
1 2
2 1
2 0Output 2
NoThis shape is an irregular pentagon. There is no way to divide it into two sections of equal area.

Input 3
5
2 0
0 4
-2 0
-2 -2
2 -2Output 3
YesWe can draw a line between and
, dividing the polygon into an isosceles triangle and a rectangle. It can be seen that the rectangle and triangle have the same area. This is illustrated below:
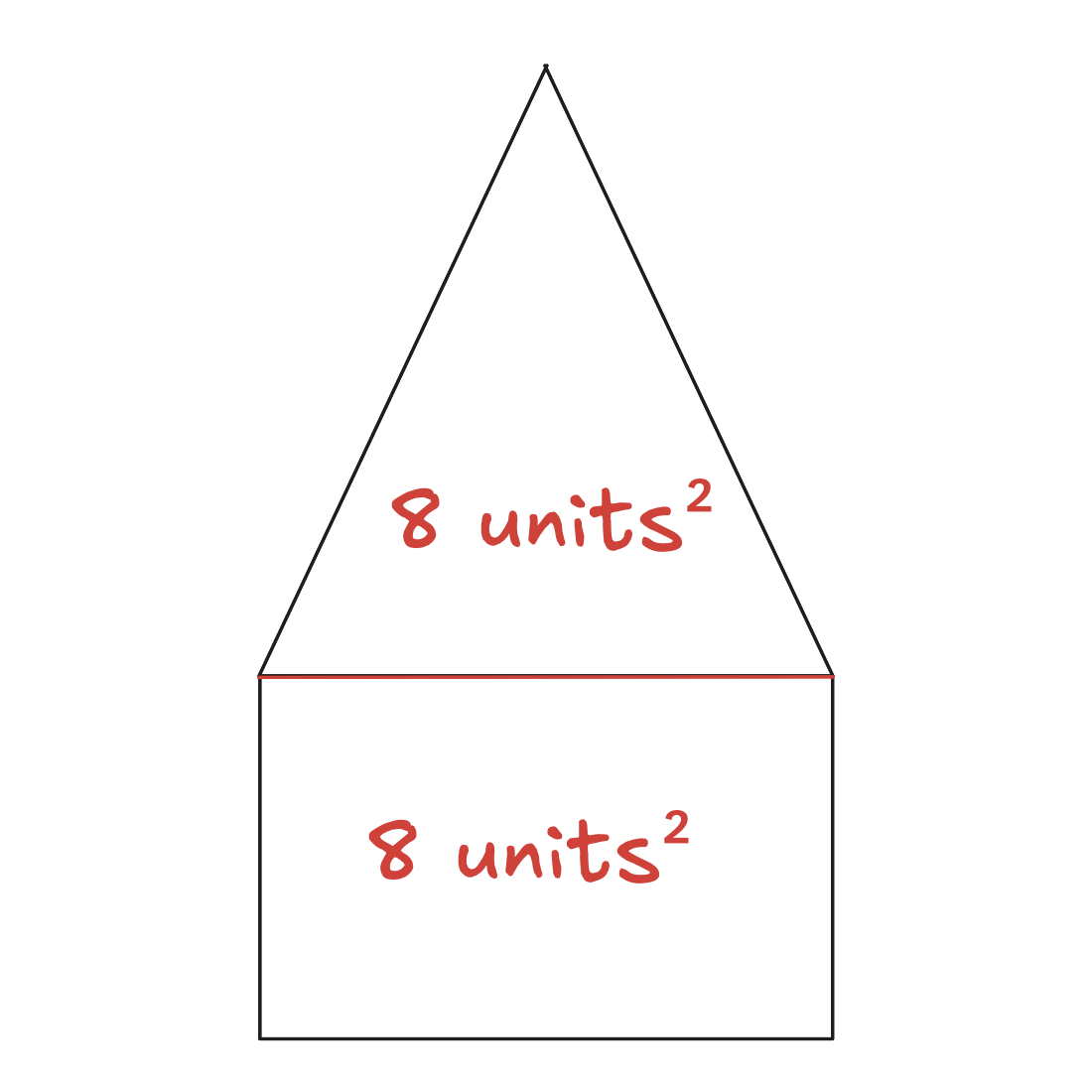
Comments