A Game of Clones
As the ruler of the Seven Kingdoms and protector of the realm, Ritisha has noticed a recurring pattern in the wars between the houses. These wars follow a unique set of rules that determine their outcome.
There are houses, numbered from
to
, each with a certain initial population
. When a war breaks out, the houses simultaneously battle in pairs:
- House 1 battles house 2.
- House 3 battles house 4.
- And so on.
The winners of each pair then move on to battle against each other in a tournament-style format, until only one house remains as the champion. The champion's population doubles, while all other houses retain their current population. Then, the next war begins.
The outcome of each battle depends on the season:
- In summer, the house with the larger population wins.
- In winter, the house with the smaller population wins.
- If their populations are the same, the leftmost house wins always.
Each set of battles lasts two seasons. If one set of battles occurs in summer, the next one will be in winter, and so on.
As protector of the realm, Ritisha wants to predict the champion of each war. Can you help her figure this out?
Input
The first line of each test case consists of two integers
, the number of houses in the realm, and
, the number of wars that break out.
is always a power of 2 (
, where
is an integer).
The next line contains integers,
, where
indicates the initial population of the
th house.
Output
For each test case, output the winner of each war.
Clarifications
- The first war begins in summer.
Example
Input 1
8 2
4 1 2 3 8 3 5 1Output 1
7
3Explanation
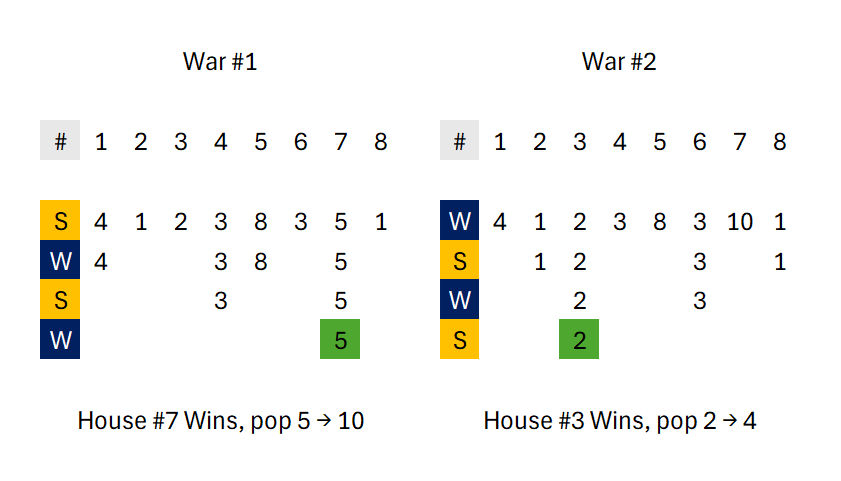
We start in summer.
War 1
- House 1 vs House 2: House 1 wins (population 4 > 1).
- House 3 vs House 4: House 4 wins (population 3 > 2).
- House 5 vs House 6: House 5 wins (population 8 > 3).
- House 7 vs House 8: House 7 wins (population 5 > 3).
Now it's winter.
- House 1 vs House 4: House 4 wins (population 3 < 4).
- House 5 vs House 7: House 7 wins (population 5 < 8).
Now it's summer again.
- House 4 vs House 7: House 7 wins (population 5 > 3).
House 7 is the champion! Its population doubles, from 5 to 10.
War 2
Now it's winter.
- House 1 vs House 2: House 2 wins (population 1 < 4).
- House 3 vs House 4: House 3 wins (population 2 < 3).
- House 5 vs House 6: House 6 wins (population 3 < 8).
- House 7 vs House 8: House 8 wins (population 1 < 10).
Now it's summer.
- House 2 vs House 3: House 3 wins (population 2 > 1).
- House 6 vs House 8: House 6 wins (population 3 > 1).
Now it's winter.
- House 3 vs House 6: House 3 wins (population 2 < 3).
House 3 is the champion! Its population doubles, from
The wars for this test case are also illustrated below:
Input 2
4 3
1 1 2 3Output 2
1
1
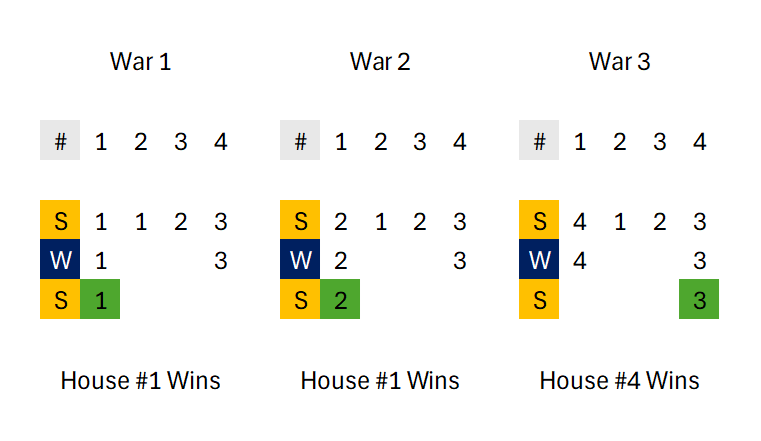
4War 1
- House 1 vs House 2: House 1 wins (population 1 = 1, number 1 < 2).
- House 3 vs House 4: House 4 wins (population 3 > 2).
Now it's winter.
- House 1 vs House 4: House 1 wins (population 1 < 3).
House 1 is the champion! Its population doubles.
War 2
Now it's summer again.
- House 1 vs House 2: House 1 wins (population 2 > 1).
- House 3 vs House 4: House 4 wins (population 3 > 2)..
Now it's winter.
- House 1 vs House 4: House 1 wins (population 2 < 3).
House 1 is the champion! Its population doubles.
War 3
Now it's summer again.
- House 1 vs House 2: House 1 wins (population 4 > 1).
- House 3 vs House 4: House 4 wins (population 3 > 2)..
Now it's winter.
- House 1 vs House 4: House 4 wins (population 4 > 3).
House 4 is the champion! Its population doubles.
The wars for this test case are also illustrated below:
Input 3
16 3
1 2 3 4 8 7 6 5 3 4 8 7 6 5 1 2Output 3
10
7
5The wars for this test case are illustrated below:
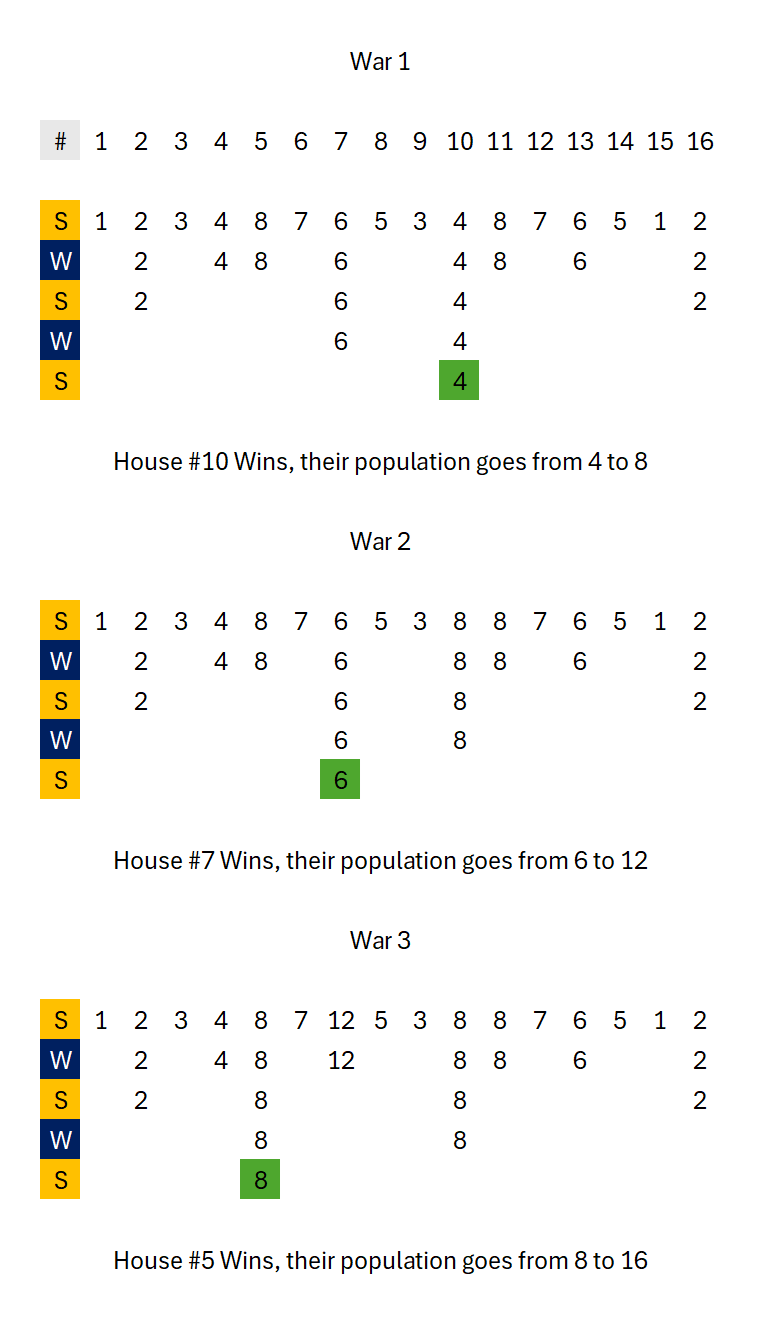
Comments